The Web as a Graph
The goal of this post is to assign an “importance score” $ x_i \in [0,1]$ to each of a set of web pages indexed $ v_i$ in a way that consistently captures our idea of which websites are likely to be important.
But before we can extract information from the structure of the internet, we need to have a mathematical description of that structure. Enter graph theory.
Definition: A web $ W$ is a directed graph $ (V, E, \varphi)$ with web pages $ v_i \in V$, hyperlinks $ e_i \in E$, and $ \varphi : E \to V \times V$ providing incidence structure.
For the remainder of this post, a web will have $ n$ pages, indexing from 1. Incoming links are commonly called backlinks, and we define the number of incoming directed edges as the in-degree of a vertex, here denoted $ \textup{in}(v_i)$. Similarly, the out-degree is the number of outgoing edges, denoted $ \textup{out}(v_i)$.
This is a very natural representation of the internet. Pages link to each other in a one-directional way. Our analysis of importance within a web will rely on a particular axiom (which we will later find dubious), that content creators usually link to websites they find important. With that in mind, the importance score of a web page should have something to do with the density of incoming links.
Of course, for simple webs this characterization is obvious. We give two examples of webs, the first of which has an obvious ranking, while the second is more ambiguous.
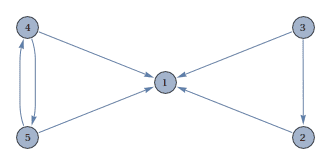
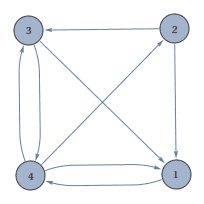
In the first web, page 1 obviously is the most important, with pages 2,4, and 5 about the same, and poor page 3 bringing up the rear. In the second, it is conceivable that there is a sensible ranking, but it is much harder to see visually.
Crawl, then Walk
As per our above discussion, our first and most naive ranking would be to just count up the in-degree of each vertex, giving the following equation to compute a page’s importance score:
$$x_i = \textup{in}(v_i)$$Unfortunately, this is not descriptive enough, and has at least one major pitfall: every link has equal value. The whole point of our ranking algorithm is to determine which websites we can trust for good content. Since “content” includes links to other content, a backlink from CNN World News should increase a page’s importance score more than a backlink from UselessJunk.com. Presently, our naive equation doesn’t capture this, but we can modify the algorithm above to reflect it. Letting $ S_i$ be the set of indices of pages with links to $ v_i$, we have
$$\displaystyle x_i = \sum\limits_{j \in S_i} x_j$$Momentarily accepting its self-referential nature (we can’t know $ x_j$ without already knowing $ x_i$), we can compute the importance score of any page as just the sum of the scores of pages which link to it. This still needs some tweaking, because here a page with a high importance score can gain too much influence simply by having a lot of links. Thus, we weight each term of the sum by the out-degree of the corresponding vertex, arriving at:
$$\displaystyle x_i = \sum\limits_{j \in S_i} \dfrac{x_j}{\textup{out}(v_j)}$$So here we have a voting system where votes correspond to links within a web, and if we can find a solution to this system of equations, we will have a sound set of rankings.
Let us do an extended example, using the second example web above (the trickier one), which we will call $ W$. If we write out the equation for each page $ v_i$, we get
$$\begin{matrix} x_1 & = & 0x_1 & + & \frac{1}{2}x_2 & + & \frac{1}{2}x_3 & + & \frac{1}{3}x_4 \\\ x_2 & = & 0x_1 & + & 0x_2 & + & 0x_3 & + & \frac{1}{3}x_4 \\\ x_3 & = & 0x_1 & + & \frac{1}{2}x_2 & + & 0x_3 & + & \frac{1}{3}x_4 \\\ x_4 & = & 1 x_1 & + & 0x_2 & + & \frac{1}{2}x_3 & + & 0x_4\end{matrix}$$This is a system of four equations with four unknowns, and so we may either solve it or prove its inconsistency. Enter linear algebra. Rewriting the system in matrix form, we wish to find a solution $ \mathbf{x} = (x_1, x_2, x_3, x_4)$ to the equation $ A \mathbf{x} = \mathbf{x}$, where $ A$, which we call the link matrix for $ W$, is as below.
$$A = \begin{pmatrix} 0 & \frac{1}{2} & \frac{1}{2} & \frac{1}{3} \\\ 0 & 0 & 0 & \frac{1}{3} \\\ 0 & \frac{1}{2} & 0 & \frac{1}{3} \\\ 1 & 0 & \frac{1}{2} & 0 \end{pmatrix}$$Look at that! Our problem of ranking pages in this web has reduced to finding an eigenvector for $ A$ corresponding to the eigenvalue 1. This particular matrix just so happens to have 1 as an eigenvalue, and the corresponding eigenvector is $ (\frac{3}{4}, \frac{1}{3},\frac{1}{2},1)$. This solution is unique up to scaling, because the eigenspace for 1, which we denote $ E_1$ is one-dimensional.
Before we continue, note that this solution is counter-intuitive: page 1 had the most incoming links, but is second in the ranking! Upon closer examination, we see that page 1 votes only for page 4, transferring its entire importance score to page 4. So along with page 3’s vote, page 4 is rightfully supreme.
The astute reader might question whether every link matrix has 1 as an eigenvalue. Furthermore, the eigenspace corresponding to 1 might have large dimension, and hence admit many different and irreconcilable rankings. For now we will sidestep both of these frightening problems with sufficiently strong hypotheses, deferring a courageous and useful solution to next time.
Assume the Scary Thoughts Away
We begin by noticing that the link matrix in the example above has non-negative entries and columns which sum to 1. Such a matrix is called column-stochastic, and it has fascinating properties. It is easy to see that if every page in a web has an outgoing link (there are no dangling nodes in the web), then the link matrix for that web is column-stochastic. We make use of this observation in the following theorem:
Theorem: The link matrix $ A$ for a web $ W$ with no dangling nodes has 1 as an eigenvalue.
Proof. Recall that $ A$ and $ A^{\textup{T}}$ have identical eigenvalues (there are many ways to prove this, try it as an exercise!). Let $ \bf{x} = (1,1, \dots , 1)$, and we see that $ A^{\textup{T}} \bf{x}$ has as its entries the sums of the rows of $ A^{\textup{T}}$, which are in turn the sums of the columns of $ A$. Since $ A$ is column-stochastic, each entry of $ A \bf{x}$ is 1, and the theorem is proved. $ \square$
So we have proven that excluding dangling nodes, the link matrix or any web has a useful ranking. Unfortunately, it is not the case that these rankings are unique up to scaling. In other words, it is not the case that every column-stochastic matrix has $ \textup{dim}(E_1)=1$. Consider the following link matrix:
$$\begin{pmatrix} 0 & 1 & 0 & 0 & 0 \\\ 1 & 0 & 0 & 0 & 0 \\\ 0 & 0 & 0 & \frac{1}{2} & \frac{1}{2} \\\ 0 & 0 & \frac{1}{2} & 0 & \frac{1}{2} \\\ 0 & 0 & \frac{1}{2} & \frac{1}{2} & 0 \end{pmatrix}$$We have two linearly independent eigenvectors $ (1,1,0,0,0), (0,0,1,1,1)$ both in $ E_1$, and so any linear combination of them is also a vector in $ E_1$. It’s not clear which, if any, we should use. Fortunately, this ambiguity exists for a good reason: the web corresponding to this link matrix has two disconnected subwebs. In real-world terms, there is no common reference frame in which to judge page 1 against page 3, so our solution space allows us to pick any frame (linear combination) we wish. In fact, it is not difficult to prove that any web which has $ m$ disconnected subwebs will admit $ \textup{dim}(E_1) \geq m$ (try it as an exercise!). In other words, we can’t prove our way to a unique ranking without some additional tweaking of the link matrix construction. Next time we will do just that.
So at this point we have solved a very restricted version of the ranking problem: we can provide sensible rankings for webs which have no dangling nodes and for which the eigenspace corresponding to the eigenvalue 1 happens to have dimension 1. Of course, in the real world, the internet has very many dangling nodes, and many disconnected subwebs. The algorithm is a home without a roof as it is (no better than a cave, really). As interesting as it is, our work so far has just been the scaffolding for the real problem.
So next time, we’ll end with a finished PageRank algorithm, code and all. Until then!
Page Rank Series
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.