Area of a Triangle

Problem: What is the area of the triangle within the rectangle?

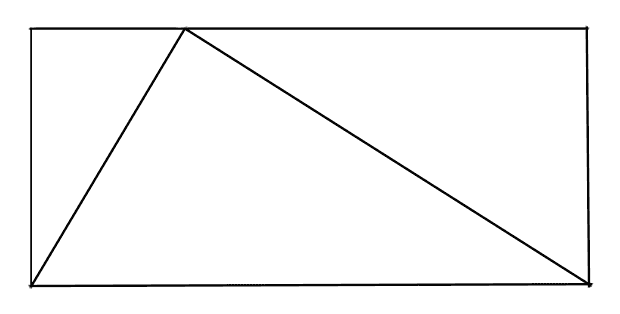
Solution: In a moment of inspiration, we draw the following additional line:

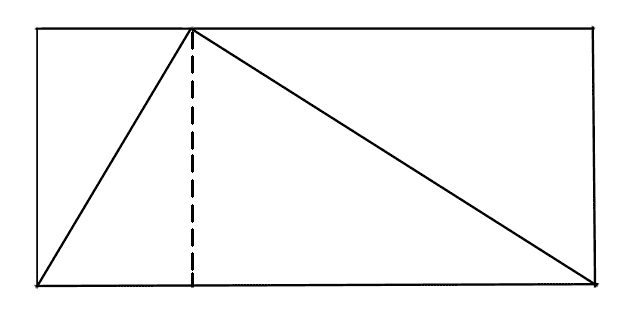
Now the answer is obvious. Once we split the rectangle into two smaller rectangles, the sides of the triangle become diagonals of their respective rectangles. The diagonals obviously split each of the two smaller rectangles into halves, where one half lies inside our original triangle. Clearly then, the interior of the whole triangle is half the area of its enclosing rectangle.

Notice that this proof holds no matter where the apex of the triangle is within the rectangle.

This proof is probably the simplest example of an elegant proof. While at first the answer is not trivial, the mathematician introduces different perspective. Here, we realize that the area of a complex figure can be determined from the sum of the areas of its parts, and that we are free to choose those parts as best suits our proof. Additional such inspirations, which experienced mathematicians call “methods,” include picking nice lines of symmetry, rotational axes, or translations of our figures to make a statement become trivial. We invite the reader, in traditional mathematical fashion, to come up with another proof of the area of a triangle using one of these different methods. Remember, the art is in the argument.