Problem: Find the sum of the first 1000 natural numbers.

Solution: Write the numbers twice as follows:

 $ \begin{matrix} 1 & + & 2 & + & \dots & + & 999 & + & 1000 \\ 1000 & + & 999 & + & \dots & + & 2 & + & 1 \end{matrix}$

Summing the numbers in each column, we have:

$ 2 (1 + 2 + \dots + 1000) = 1001 + 1001 + \dots + 1001$ (1000 times)

And dividing by two we have

$ 1 + 2 + \dots + 1000 = \frac{1000 * 1001}{2} = 500500$

This method clearly works not just for 1000, but any natural number $ n$.

Problem: Find the sum of the squares of the first $ n$ natural numbers

Solution: Arrange the numbers three times, in triangles as follows:

Arranging the numbers in triangles, where each summand is successively rotated 120 degrees.

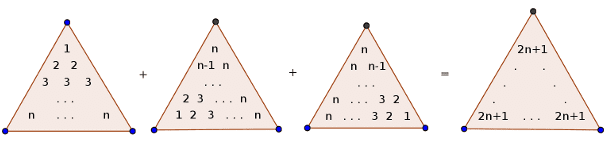
Here we prove what is obvious from the picture: that the numbers in the “sum” triangle work out as expected.

In the leftmost triangle, there are $ i$ copies of $ i$ in the $ i$th row (indexing from 1), so the sum of the $ i$th row is $ i^2$, and the sum of all the numbers in the triangle is $ (1^2 + 2^2 + \dots + n^2)$. Since the other two “summand” triangles are just rotations of the first triangle, their sums are also the sum of the first $ n$ squares.

In the “sum” triangle at the $ i$th row $ j$ spaces from the left (indexing both from zero), we have the value $ (1+i) + (n-i+j) + (n-j) = 2n+1$. In each triangle there are $ 1 + 2 + \dots + n = \frac{n(n+1)}{2}$ different numbers (as per the first proof), so there are that many copies of $ 2n+1$ in the fourth triangle. Summing up the fourth triangle gives three times our desired result, and hence

$ 3(1^2 + 2^2 + \dots + n^2) = \frac{n(n+1)(2n+1)}{2}$, or
$ (1^2+2^2+\dots + n^2) = \frac{n(n+1)(2n+1)}{6}$

This second proof was shown to me by Sándor Dobos, a professor of mine in Budapest whom I remember fondly.