“Tonight’s the Night”
A large volume of research goes into the psychological and behavioral analysis of criminals. In particular, serial criminals hold a special place in the imagination and nightmares of the general public (at least, American public). Those criminals with the opportunity to become serial criminals are logical, cool-tempered, methodical, and, of course, dangerous. They walk among us in crowded city streets, or drive slowly down an avenue looking for their next victim. They are sometimes neurotic sociopaths, and other times amicable, charming models of society and business. But most of all, they know their craft well. They work slowly enough to not make mistakes, but fast enough to get the job done and feel good about it. Their actions literally change lives.
In other words, they would be good programmers. If only they all hadn’t given up trying to learn C++!
In all seriousness, a serial killer’s rigid methodology sometimes admits itself nicely to mathematical analysis. For an ideal serial criminal (ideal in being analyzable), we have the following two axioms of criminal behavior:
- A serial criminal will not commit crimes too close to his base of operation.
- A serial criminal will not travel farther than necessary to find victims.
The first axiom is reasonable because a good serial criminal does not want to arouse suspicion from his neighbors. The second axiom roughly describes an effort/reward ratio that keeps serial offenders from travelling too far away from their homes.
These axioms have a large amount of criminological research behind them. While there is little unifying evidence (the real world is far too messy), there are many bits and pieces supporting these claims. For example, the frequency of burglaries peak about a block from the offender’s residence, while almost none occur closer than a block (Turner, 1969, “Delinquency and distance”). Further, many serial rapists commit subsequent rapes (or rather, abductions preceding rape) within a half mile from the previous (LeBeau, 1987, “Patterns of stranger and serial rape offending”). There are tons of examples of these axioms in action in criminology literature.
On the other hand, there are many types of methodical criminals who do not agree with these axioms. Some killers murder while traveling the country, while others pick victims with such specific characteristics that they must hunt in a single location. So we take the following models with a grain of salt, in that they only apply to a certain class of criminal behavior.
With these ideas in mind, if we knew a criminal’s base of operation, we could construct a mathematical model of his “buffer zone,” inside of which he does not commit crime. With high probability, most of his crimes will lie just outside the buffer zone. This in itself is not useful in the grand scheme of crime-fighting. If we know a criminal’s residence, we need not look any further. The key to this model’s usefulness is working in reverse: we want to extrapolate a criminal’s residence from the locations of his crimes. Then, after witnessing a number of crimes we believe to be committed by the same person, we may optimize a search for the offender’s residence. We will use the geographic locations of a criminal’s activity to accurately profile him, hence the name, geoprofiling.
Murder, She Coded
Historically, the first geoprofiling model was crafted by a criminologist named Dr. Kim Rossmo. Initially, he overlaid the crime locations on a sufficiently fine $ n \times m$ grid of cells. Then, he uses his model to calculate the probability of the criminal’s residence lying within each cell. Rossmo’s formula is displayed below, and explained subsequently.
$ \displaystyle P(x) = \sum \limits_{\textup{crime locations } c} \frac{\varphi}{d(x,c)^f} + \frac{(1-\varphi)B^{f-g}}{(2B-d(x,c))^g}$,
where $ \varphi = 1$ if $ d(x,c) > B, 0$ otherwise.
Here, $ x$ is an arbitrary cell in the grid, $ d(x,c)$ is the distance from a cell to a crime location, with some fixed metric $ d$. The variable $ \varphi$ determines which of the two summands to nullify based on whether the cell in question is in the buffer zone. $ B$ is the radius of the buffer zone, and $ f,g$ are formal empirically tuned parameters. Variations in $ f$ and $ g$ change the steepness of the decay curve before and after the buffer radius. We admit to have no idea why they need to be related, and cannot find a good explanation in Rossmo’s novel of a dissertation. Instead, Rossmo claims both parameters should be equal. For the purposes of this blog we find their exact values irrelevant, and put them somewhere between a half and two thirds.
This model reflects the inherent symmetry in the problem. If we may say that an offender commits a crime outside a buffer of some radius $ B$ surrounding his residence, then we may also say that the residence is likely outside a buffer of the same radius surrounding each crime! For a fixed location, we may compute the probability of the offender’s residence being there with respect to each individual crime, and just sum them up.
This equation, while complete, has a better description for programmers, which is decidedly easier to chew in small bites:
Let d = d(x,c)
if d > B:
P(x) += 1/d^f
else:
P(x) += B^(f-g)/(2B-d)^g
Then we may simply loop this routine over over all such $ c$ for a fixed $ x$, and get our probability. Here we see the ideas clearly, that outside the buffer zone of the crime the probability of residence decreases with a power-law, and within the buffer zone it increases approaching the buffer.
Now, note that these “probabilities” are not, strictly speaking, probabilities, because they are not normalized in the unit interval $ [0,1]$. We may normalize them if we wish, but all we really care about are the relative cell values to guide our search for the perpetrator. So we abuse the term “high probability” to mean “relatively high value.”
Finally, the distance metric we actually use in the model is the so-called taxicab metric. Since this model is supposed to be relevant to urban serial criminals (indeed, where the majority of cases occur), the taxicab metric more accurately describes a person’s mental model of distance within a city, because it accounts for roadways. Note that in order for this to work as desired, the map used must be rotated so that its streets lie parallel to the $ x,y$ axes. We will assume for the rest of this post that the maps are rotated appropriately, as this is a problem with implementation and not the model itself or our prototype.
Rossmo’s model is very easy to implement in any language, but probably easiest to view and animate in Mathematica. As usual, the entire program for the examples presented here is available on this blog’s Github page. The decay function is just a direct translation of the pseudocode:
rossmoDecay[p1_, p2_, bufferLength_, f_, g_, distance_] :=
With[{d = distance[p1, p2]},
If[d > bufferLength,
1/(d^f),
(bufferLength^(g - f))/(2 bufferLength - d)^g]];
We then construct a function which computes the decay from a fixed cell for each crime site:
makeRossmoFunction[sites_, buffer_, f_, g_] :=
Function[{x, y},
Apply[Plus,
Map[rossmoDecay[#,{x,y},buffer,f,g,ManhattanDistance] &,
sites]]];
Now we may construct a “Rossmo function,” (initializing the parameters of the model), and map the resulting function over each cell in our grid:
Array[makeRossmoFunction[sites, 14, 1/3, 2/3], {60, 50}];
Here the Array function accepts a function $ f$, and a specification of the dimensions of the array. Then each array index tuple is fed to $ f$, and the resulting number is stored in the $ i,j$ entry of the array. Here $ f: \mathbb{Z}_{60} \times \mathbb{Z}_{50} \to \mathbb{R}^+$. We use as a test the following three fake crime sites:
sites = {{20, 25}, {47, 10}, {55, 40}};
Upon plotting the resulting array, we have the following pretty picture:

Here, the crime locations are at the centers of each of the diamonds, and cells with more reddish colors have higher values. Specifically, the “hot spot” for the criminal’s residence is in the darkest red spot in the bottom center of the image.
As usual, in order to better visualize the varying parameters, we have the following two animations:


Variation in the $ B$ parameter simply increases or decreases the size of the buffer zone. In both animations above we have it fixed at 14 units.
Despite the pretty pictures, a mathematical model is nothing without empirical evidence to support it. Now, we turn to an analysis of this model on real cases.
“Excellent!” I cried. “Elementary mathematics,” said he.
Richard Chase
The first serial killer we investigate is Richard Chase, also known as the Vampire of Sacramento. One of the creepiest murderers in recent history, Richard Chase believed he had to drink the blood of his victims in order to live. In the month of January 1978, Chase killed five people, dumping their mutilated bodies in locations near his home.
Before we continue with the geographic locations of this particular case, we need to determine which locations are admissible. For instance, we could analyze abduction sites, body drop sites, locations of weapons caches or even where the perpetrator’s car was kept. Unfortunately, many of these locations are not known during an investigation. At best only approximate abduction sites can be used, and stash locations are usually uncovered after an offender is caught.
For the sake of the Chase case, and subsequent cases, we will stick to the most objective data points: the body drop sites. We found this particular data in Rossmo’s dissertation, page 272 of the pdf document. Overlaid on a 30 by 30 grid, they are:lib-ib-r
richardChaseSites =
{{3, 17}, {15, 3}, {19, 27}, {21, 22}, {25, 18}};
richardChaseResidence = {19,17};
Then, computing the respective maps, we have the following probability map:
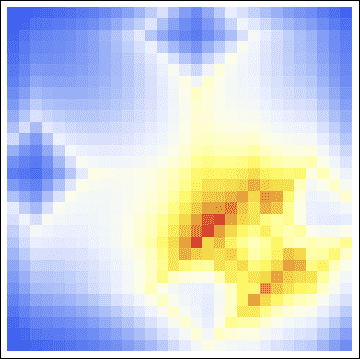
If we overlay the location of Chase’s residence in purple, we see that it is very close to the hottest cell, and well-within the hot zone. In addition, we compare this with another kind of geoprofile: the center of gravity of the five sites. We color the center of gravity in black, and see that it is farther from Chase’s residence than the hot zone. In addition, we make the crime sites easy to see by coloring them green.

Albert DeSalvo
This is a great result for the model! Let us see how it fares on another case: Albert DeSalvo, the Boston strangler.
With a total of 13 murders and being suspected of over 300 sexual assault charges, DeSalvo is a prime specimen for analysis. DeSalvo entered his victim’s homes with a repertoire of lies, including being a maintenance worker, the building plumber, or a motorist with a broken-down car. He then proceeded to tie his victims to a bed, sexually assault them, and then strangle them with articles of clothing. Sometimes he tied a bow to the cords he strangled his victims with.
We again use the body drop sites, which in this case are equivalent to encounter sites. They are:
deSalvoSites = {{10, 48}, {13, 8}, {15, 11}, {17, 8}, {18, 7},
{18, 9}, {19, 4}, {19, 8}, {20, 9}, {20, 10}, {20, 11},
{29, 23}, {33, 28}};
deSalvoResidence = {19,18};
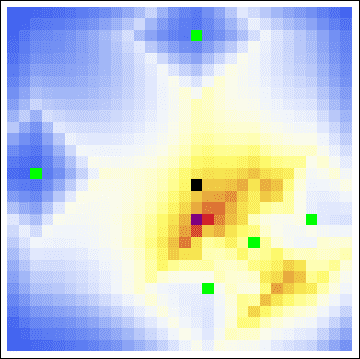
Running Rossmo’s model again, including the same extra coloring as for the Chase murders, we get the following picture:
Again, we win. DeSalvo’s residence falls right in the darker of our two main hot zones. With this information, the authorities would certainly apprehend him in a jiffy. On the other hand, the large frequency of murders in the left-hand side pulls the center of gravity too close. In this way we see that the center of gravity is not a good “measure of center” for murder cases. Indeed, it violates the buffer principle, which holds strong in these two cases.

Peter Sutcliffe
Finally, we investigate Peter Sutcliffe, more infamously known as the Yorkshire Ripper. Sutcliffe murdered 13 women and attacked at least 6 others between 1975 and 1980 in the county of West Yorkshire, UK. He often targeted prostitutes, hitting them over the head with a hammer and proceeding to sexually molest and mutilate their bodies. He was finally caught with a prostitute in his car, but was not initially thought to be the Yorkshire Ripper until after police returned to the scene of his arrest to look for additional evidence. They found his murder weapons, and promptly prosecuted him.
We list his crime locations below. Note that these include body drop sites and the attack sites for non-murders, which were later reported to the police.
sutcliffeSites = {{5, 1}, {8, 7}, {50, 99}, {53, 68}, {56, 72},
{59, 59}, {62, 57}, {63, 85}, {63, 87}, {64, 83}, {69, 82},
{73, 88}, {80, 88}, {81, 89}, {83, 88}, {83, 87}, {85, 85},
{85, 83}, {90, 90}};
sutcliffeResidences = {{60, 88}, {58, 81}};
Notice that over the course of his five-year spree, he lived in two residences. One of these he moved to with his wife of three years (he started murdering after marrying his wife). It is unclear whether this changed his choice of body drop locations.
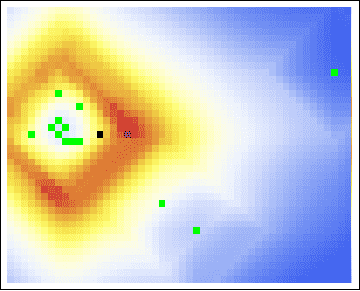
Unfortunately, our attempts to pinpoint Sutcliffe’s residence with Rossmo’s model fail miserably. With one static image, guessing at the buffer radius, we have the following probability map:
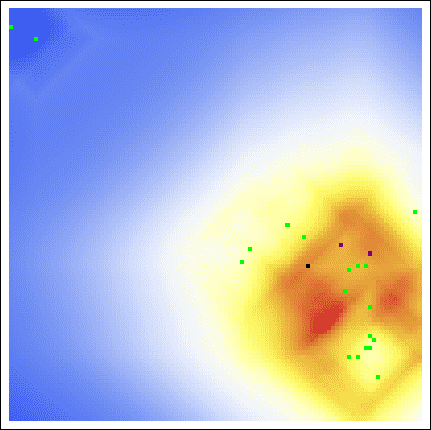
As we see, both the center of gravity and the hot zones are far from either of Sutcliffe’s residences. Indeed, even with a varying buffer radius, we are still led to search in unfruitful locations:
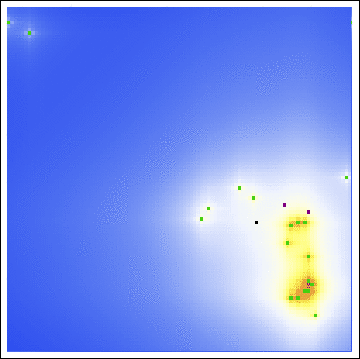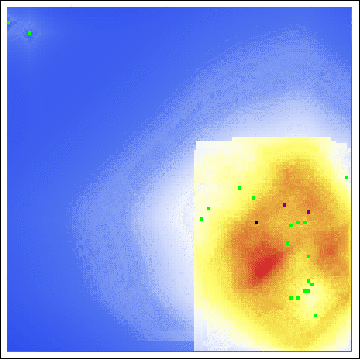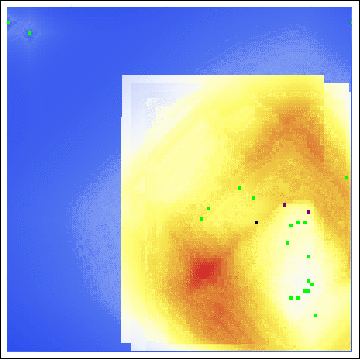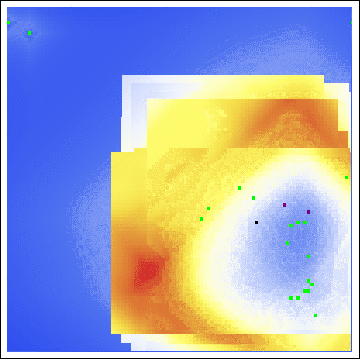
Even with all of the axioms, all of the parameters, all of the gosh-darn work we went through! Our model is useless here. This raises the obvious question, exactly how applicable is Rossmo’s model?
The Crippling Issues
The real world is admittedly more complex than we make it out to be. Whether the criminal is misclassified, bad data is attributed, or the killer has some special, perhaps deranged motivation, there are far too many opportunities for confounding variables to tamper with our results. Rossmo’s model even requires that the killer live in a more or less central urban location, for if he must travel in a specific direction to find victims, he may necessarily produce a skewed distribution of crime locations.
Indeed, we have to have some metric by which to judge the accuracy of Rossmo’s model. While one might propose the distance between the offender’s residence and the highest-probability area produced on the map, there are many others. In particular, since the point of geographic profiling is to prioritize the search for a criminal’s residence, the best metric is likely the area searched before finding the residence. We call this metric search area. In other words, search area is the amount of area on the map which has probability greater or equal to the cell containing the actual residence. Indeed Rossmo touts this metric as the only useful metric.
However, according to his own tests, the amount of area searched on the Sutcliffe case would be over a hundred square miles! In addition, Rossmo neither provides an idea of what amount of area is feasibly searchable, nor any global statistics on what percentage of cases in his study resulted in an area that was feasibly searchable. We postulate our own analysis here.
In a count of Rossmo’s data tables, out of the fifteen individual cases he studied, the average search area was 395 square kilometers, or 152.5 square miles, while the median was about 87 square kilometers, or 33.6 square miles. The maximum is 1829 square kilometers, while the min is 0.2 square kilometers. The complete table is contained in the Mathematica notebook on this blog’s Github page.
From the 1991 census data for Vancouver, we see that a low density neighborhood has an average population of 2,380 individuals per square kilometer, or about 6,000 per square mile. Applying this to our numbers from the previous paragraph, we have a mean of 940,000 people investigated before the criminal is found, a median of 200,000, a max of four million (!), and a min of 309.
Even basing our measurements on the median values, this method appears to be unfeasible as a sole means of search prioritization. Of course, real investigations go on a lot more data, including hunches, to focus search. At best this could be a useful tool for police, but on the median, we believe it would be marginally helpful to authorities prioritize their search efforts. For now, at least, good ol’ experience will likely prevail in hunting serial killers.
In addition, other researchers have tested human intuition at doing the same geographic profiling analysis, and they found that with a small bit of training (certainly no more than reading this blog post), humans showed no significant difference from computers at computing this model. (English, 2008) Of course, for the average human the “computing” process (via pencil and paper) was speedy and more variable, but for experienced professionals the margin of error would likely disappear. As interesting as this model may be, it seems the average case is more like Sutcliffe than Chase; Rossmo’s model is effectively a mathematical curiosity.
It appears, for now, that our friend Dexter Morgan is safe from the threat of discovery by computer search.
Alternative Models
The idea of a decay function is not limited to Rossmo’s particular equation. Indeed, one might naturally first expect the decay function to be logarithmic, normal, or even exponential. Indeed, such models do exist, and they are all deemed to be roughly equivalent in accuracy for appropriately tuned parameters. (English, 2008) Furthermore, we include an implementation of a normal growth/decay function in the Mathematica notebook on this blog’s Github page. After reading that all of these models are roughly equivalent, we did not conduct an explicit analysis of the normal model. We leave that as an exercise to the reader, in order to become familiar with the code provided.
In addition, one could augment this model with other kinds of data. If the serial offender targets a specific demographic, then this model could be combined with demographic data to predict the sites of future attacks. It could be (and in some cases has been) weighted according to major roadways and freeways, which reduce a criminals mental model of distance to a hunting ground. In other words, we could use the Google Maps “shortest trip” metric between any two points as its distance metric. To our knowledge, this has not been implemented with any established mapping software. We imagine that such an implementation would be slow; but then again, a distributed network of computers computing the values for each cell in parallel would be quick.
Other Uses for the Model
In addition to profiling serial murders, we have read of other uses for this sort of geographic profiling model.
First, there is an established paper on the use of geographic profiling to describe the hunting patterns of great white sharks. Briefly, we recognize that such a model would switch from a taxicab metric to a standard Euclidean metric, since the movement space of the ocean is locally homeomorphic to three-dimensional Euclidean space. Indeed, we might also require a three-dimensional probability map for shark predation, since sharks may swim up or down to find prey. Furthermore, shark swimming patterns are likely not uniformly random in any direction, so this model is weighted to consider that.
Finally, we haphazardly propose additional uses for this model: pinpointing the location of stationary artillery, locating terrorist base camps, finding the source of disease outbreaks, and profiling other minor serial-type criminals, like graffiti vandalists.
Data! Data! My Kingdom for Some Data!
As recent as 2000, one researcher noted that the best source of geographic criminal data was newspaper archives. In the age of information, and given the recent popularity of geographic profiling research, this is a sad state of being. As far as we know, there are no publicly available indexes of geographic crime location data. As of the writing of this post, an inquiry to a group of machine learning specialists has produced no results. There doesn’t seem to be such a forum for criminology experts.
If any readers have information to crime series data that is publicly available on the internet (likely used in some professor’s research and posted on their website), please don’t hesitate to leave a comment with a link. It would be greatly appreciated.
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.
