Tiling a Chessboard with Dominoes (Opposite Colors Removed)

This is a natural follow-up to our first gallery entry on the impossibility of tiling certain chessboards with dominoes.

Problem: Suppose we remove two squares from a chessboard which have opposite color. Is it possible to tile the remaining squares with 2-by-1 dominoes?

Solution:

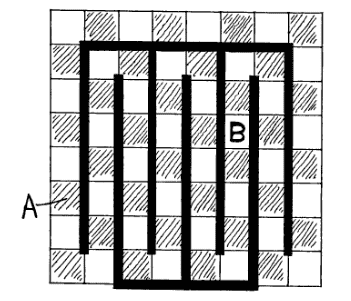
Notice that if we remove two squares of opposite color, then there is only one way to place dominoes on the remaining squares according to this scheme (one cannot tile a domino across the “walls”). Removing two squares of opposite color ensures there is an even number of squares between the removed squares, and so the dominoes will fit as desired. In other words, the two “paths” from A to B, starting on any side of A, contain an even number of squares, and so placing a domino every two squares will fill the path with a good tiling.

Not only does this method provide a positive answer to the solution, it gives a constructive answer. If we had some odd desire to do so, we could write an algorithm which tiles any chessboard where two squares are removed, (moreover, it would run in linear time). It’s not obvious at first whether such an algorithm exists, as the average human attempt to tile a board with two random squares removed would likely require some backtracking. In other words, human solutions would generally be heuristic in nature, but this analysis gives a solution that any person could utilize.