Other Complexity Classes

Not Just Time, But Space Too!

So far on this blog we’ve introduced models for computation, focused on Turing machines and given a short overview of the two most fundamental classes of problems: P and NP. While the most significant open question in the theory of computation is still whether P = NP, it turns out that there are hundreds (almost 500, in fact!) other “classes” of problems whose relationships are more or less unknown.

For instance, we can ask about problems that can be solved using polynomially-bounded space instead of time. This class would be called “PSPACE,” and it’s easy to see that $ \textup{P} \subset \textup{PSPACE}$. As usual, there is a corresponding notion of problems solvable with polynomial-bounded space on a nondeterministic Turing machine, having the likely name NPSPACE. One might expect another huge open question: does PSPACE = NPSPACE? It turns out they are equal, and this just goes to show how sometimes nondeterminism doesn’t allow us to “do more” in one sense, but it does in another.

Another interesting question is the computational complexity of problems in the presence of oracles. Suppose we had a magical machine that could solve some difficult or impossible problem (say, the Halting Problem) in constant time. Then what sorts of problems can be solved in polynomial time? This notion gives rise to a whole new family of complexity classes that rely critically on using the oracle.

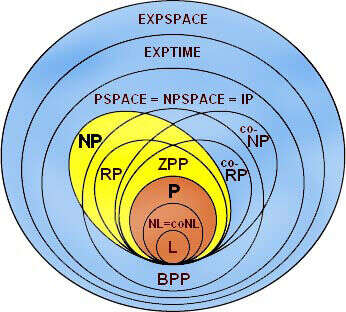
Above we give an example of some believed relationships between some basic complexity classes (I say basic, but even I haven’t ever heard of ZPP before). In a simplistic mindset, the goal of computing theory as a field of mathematics is to determine all of the relationships between these classes. In other words, we want to be able to answer all questions like, “Is computation with logarithmically-bounded space fundamentally different from computation with polynomially-bounded time?” Tacking this on to the fat list of open questions like P vs. NP, we admit that nobody knows the answer.

Unfortunately a primer on any more of these complexity classes would take us too far from the scope of this blog. We hardly skimmed the surface on P and NP, leaving quite a bit of low-hanging fruit to speculation (like, is there a problem which is not in NP? Or more subtly, is there a problem which is in NP, but not NP-complete? There is such a problem, but as far as this author knows, there is no known naturally occurring problem).

But fear not, interested reader! Even if we can’t reasonably commit to cataloging more complexity classes here, we do have an excellent reference: the Complexity Zoo. This is a more or less complete list of all known complexity classes, with pages and pages of descriptions and documented relationships with links to papers. Browsing the front-page list of classes, we see such intriguing and mysterious names as “Almost-PSPACE,” and “HeuristicP,” and “Quantum Refereed Games.”

The novice reader should start with the Petting Zoo, which expands on our meager introduction by describing, mostly in informal terms, the twenty most important complexity classes, and providing awesome inclusion graphs like the one below:

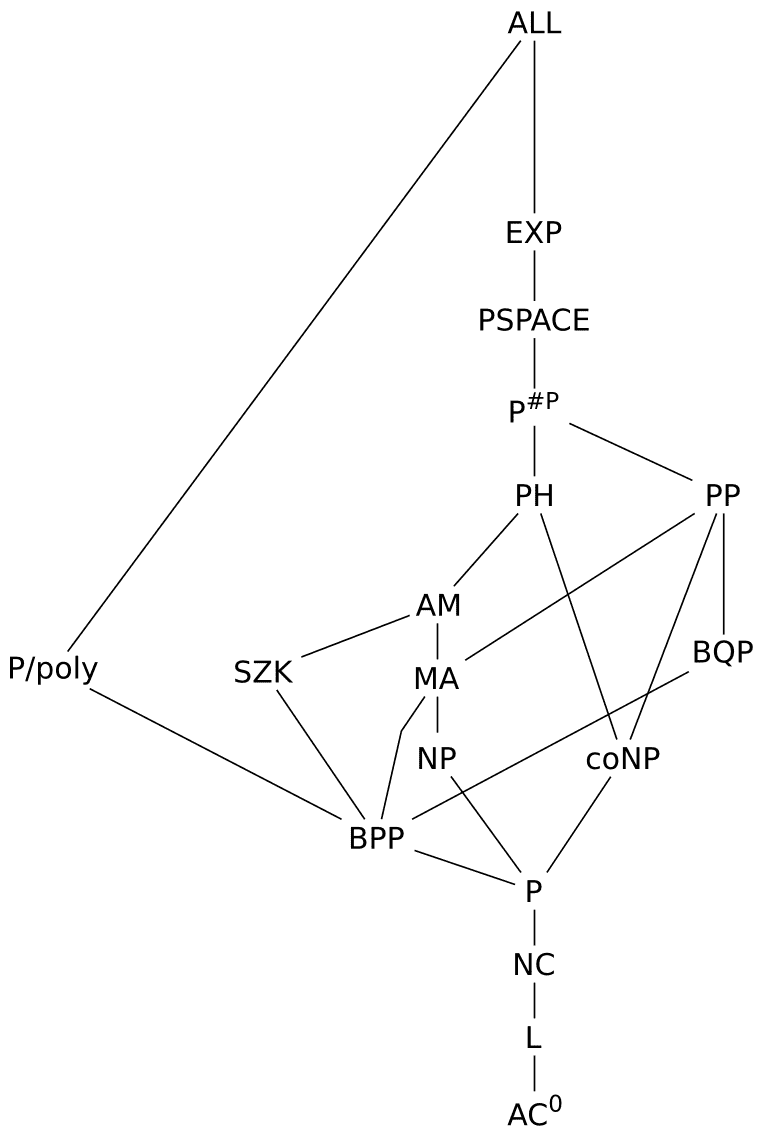
The project was conceived and is organized by Scott Aaronson, a prominent researcher at MIT (with a neat blog of his own, though it’s pretty difficult material when he talks about his own research in quantum circuits). The Zoo also has a small side-exhibit focusing on the problems themselves, which is called the Complexity Garden. For instance he covers the quintessential NP-complete problem that we mentioned last time, namely N-Satisfiability.

Here on this blog we do have one more primer in the realm of Complexity Theory planned, but it’s more a question about data than Turing machines. I will introduce the notion of Kolmogorov complexity, and prove a few of its basic and interesting properties.

Until then!