The study of groups is often one’s first foray into advanced mathematics. In the naivete of set theory one develops tools for describing basic objects, and through a first run at analysis one develops a certain dexterity for manipulating symbols and definitions. But it is not until the study of groups that one must step back and inspect the larger picture. The main point of that picture (and indeed the main point of a group) is that algebraic structure can be found in the most unalgebraic of settings. And we mean algebraic literally: we will make sense of what it means to “multiply” things which are not even close to numbers.

It is in my mind prohibitively difficult to motivate the study of these sorts of abstract algebraic objects. Part of the problem is that in order to impress upon the reader any hint of the riches returned from investing in their study, one must already be fluent in their language (indeed, in their culture!) and recognize the commanding utility of discovering them in otherwise mysterious places.

In pure mathematics, the study of groups alone has yielded some impressive and counterintuitive results:

And there are plenty of applications to the real world:

As a general rule, anything which has some kind of symmetrical structure can be “represented” by a group. We will of course make these notions clearer in this post, but before we jump into the rigorous mathematics, let us give two accessible (visual) examples of groups.

The Square and the Rubik’s Cube

Imagine a square in the plane:

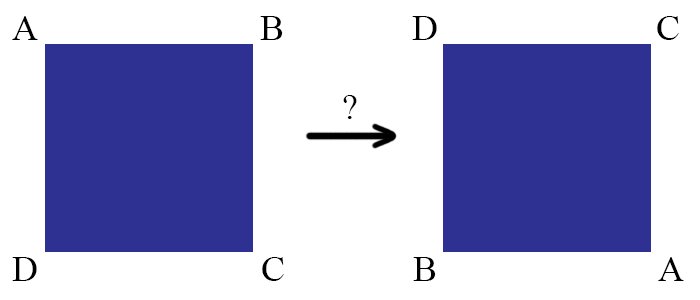
Specifically, we will label each of the corners of this square so that we can distinguish them from another. One can imagine cutting this square out of the plane, doing some kind of physical manipulation, and placing it back into the same hole (so that it fills up all the same space). For instance, one can rotate the square by a quarter turn (say, counterclockwise), or reflect it across a diagonal (say, the AC diagonal) before replacing it. Either of these two operations will not alter the square itself: it will always take points in the square to other points in the square. In other words, it might be the case that our four labelled corners are swapped around, but if we had not labelled the corners we wouldn’t be able to tell anything had changed. More rigorously, these transformations have to preserve the distances between points, so we cannot stretch, tear, or squeeze the square in any way.

If we denote a quarter-turn rotation by $ \rho$ and a flip by $ \sigma$, we can write down a sequence of these operations like

$$\rho \sigma \rho \rho$$

Where we apply the operations in order from left to right. That is, the above operation is “rotate a quarter turn, then flip, then rotate twice more.” Using the same notation: here are some additional examples of these operations on the square:

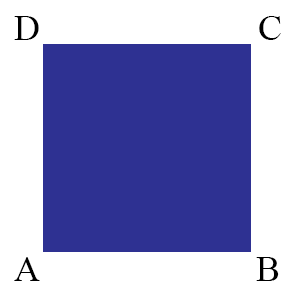
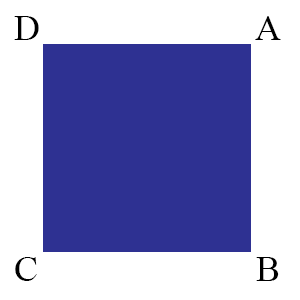
In particular, we will call one of these operations a symmetry of the square. Now we can ask the following question, “How can we classify all of the different kinds of symmetry of the square?”

There are some obvious properties of these symmetries. First, and trivially, the operation where we “do nothing” is a valid symmetry. Second, each of these symmetries has an “opposite” symmetry. Indeed, in terms of sets these symmetries are functions, and they should be bijections. And finally, as we’ve already seen, we can compose any two symmetries to get another symmetry.

The salient point here is that two different compositions of symmetries can end up being the same thing. Indeed, doing the same flip twice is the same thing as doing nothing, and rotating four times is also the same thing as doing nothing.

Moreover, a symmetry of the square is completely determined by how it moves the corners around. Here’s a short sketch of a proof of this. By our requirement that distances are preserved, the corners must also go to corners (think of the diagonal corners), and once the corners are chosen every other point in the square is required to be a certain distance from each corner. A standard geometric argument shows that three or more circles with non-collinear centers which have a simultaneous intersection point must intersect in a single point.

And so there is a one-to-one correspondence between symmetries of the square and the pictures of the resulting squares with labels. The important fact is that not all possible labelings can be represented in this way. For example, the reader will try in vain to find a symmetry between the two labeled squares:

We will touch more on this example later, but here’s a more complicated example.

A Rubik’s Cube (Wikipedia)

In the same way that we can enumerate all possible symmetries of the square, we can enumerate all possible symmetries of the Rubik’s cube. But here the structure is more complicated: we can rotate any one of the six faces of the cube, and the relationships between operations are not at all obvious. The colored stickers form our labels to distinguish two configurations, but it’s not clear which (if any) stickers are superfluous. But again the same properties hold: there is a do-nothing operation, every operation is reversible, and any two operations can be composed and the result is still a valid operation.

As we will see shortly, these properties characterize what it means to have symmetry.

Groups

Now that we’ve seen two examples of symmetry groups, it’s time to get abstract. The three properties of symmetries we mentioned above will form the basis for our definition:

Definition: A group $ G$ is a set with a specified binary operation (denoted here by a $ \cdot$), so that the following properties hold:

There are a few issues we need to get out of the way about this definition and the mess of notation associated with it, but first let’s see some trivial examples.

The singleton set $ \left \{ e \right \}$ with the binary operation $ \cdot$ defined by setting $ e \cdot e = e$ is trivially a group. In terms of symmetries there is only one operation (to do nothing), and doing nothing any number of times is the same as doing nothing.

The set of integers $ \mathbb{Z}$ forms a group under the operation of addition. It is common knowledge that zero fits the definition of the identity element, that the sum of two integers is an integer, that addition on integers is associative, and that every integer has an additive inverse. We can similarly take any of our common number systems and see that they are groups under addition: rational numbers, real numbers, complex numbers, etc. IF we want to work with multiplication, it is not hard to see that $ \mathbb{R} – \left \{ 0 \right \}$ is a group, since every nonzero real number has an inverse, and 1 is the multiplicative identity.

Here are a few basic propositions to clear up some silly ambiguities in the definition. For instance, we never say that there should only be one identity element. But indeed, if there are two identity elements $ e, e’$, then we can show they must be equal:

$$e = e \cdot e’ = e’$$

The first equality holds because $ e’$ is an identity element, and the second because $ e$ is. A similar proof shows that the inverse of an element is unique. Therefore, we are justified in the following notation: we will call the identity element $ 1$, and use subscripts $ 1_G, 1_H$ to distinguish between identity elements in different groups $ G, H$. We will also conventionally replace the explicit $ \cdot$ operation with juxtaposition, and emulate the multiplication operation by saying things like $ x^n$ to mean $ x \cdot x \cdot \dots \cdot x$ multiplying $ n$ times.

Of course, if we’re talking about the integers $ \mathbb{Z}$ that won’t do, because $ \mathbb{Z}$ is only a group under addition (although multiplication is well-defined, only $ \pm 1$ have multiplicative inverses). So in the case of groups whose underlying sets are numbers, we have to be more careful. In these cases, we will write things like $ nx$ to mean $ x + x + \dots + x$ adding $ n$ times (and here $ n$ is not considered an element of $ \mathbb{Z}$ as a group, but just the number of additions), and $ -x$ for the additive inverse of $ x$. While all of this notation might sound horribly confusing, we promise that it’s easy to get used to.

Another preliminary question we might ask is: are there groups of any given set size?

Definition: The order of a group, denoted $ |G|$, is the size of $ G$ as a set. If $ G$ is an infinite set, we say it has infinite order. Otherwise we say it has finite order.

Just as a quick example, let’s take the group of integers modulo 4. That is, our set is $ \left \{ 0, 1, 2, 3 \right \}$, and the operation $ +$ is defined by adding the two operands and taking the remainder when dividing by four. It is easy to verify this is indeed a group, and it has order 4. In addition this group is equivalent to the structure of rotations of our square earlier. In particular, if we consider the do-nothing operation to be 0, a quarter turn to be the number 1, a half turn to be 2, and a three-quarter turn to be 3, then composing two rotations would correspond to addition between the two numbers, where a full 360-degree rotation is the same as doing nothing. In the formal parlance, which we’ll explain shortly, these two groups are isomorphic. Everything about their group structure is the same, they just have different labels for their elements and operations.

The number 4 is obviously arbitrary. We could define $ \mathbb{Z}/n\mathbb{Z}$ to be the group of integers modulo $ n$ for any $ n$. And it’s not hard to see that this group is isomorphic to the group of rotations of the regular $ n$-gon in the plane. So there are finite groups of any order we please, and we can realize them as the rotational groups of regular polygons.

These groups $ \mathbb{Z}$ and $ \mathbb{Z}/n\mathbb{Z}$ share something else in common: their operations are commutative. That is, for any two integers $ x+y = y+x$ (regardless of whether we take modulus afterward). It is not hard to see that group operations are not always commutative, because we have already seen one. The symmetry group of the square, if we call $ \rho$ a quarter turn and $ \sigma$ a diagonal flip, it will not be true that $ \rho \sigma = \sigma \rho$.

Definition: A group $ G$ is called abelian (pronounced, uh-BEE-lee-un) if its group operation is commutative.

Abelian groups are quite important. Part of the reason is that finite abelian groups are completely understood. This is a standard statement of classification, and it is one of the main results of group theory. We are not yet equipped to state or prove it, but in principle the idea is clear: every finite abelian group decomposes into pieces that look like $ \mathbb{Z}$ and $ \mathbb{Z}/n\mathbb{Z}$ for some choices of $ n$.

Before we continue we should note a few other examples of groups which come up quite often:

Subgroups, Group Homomorphims, and Quotients

Definition: Let $ (G, \cdot)$ be a group and let $ H \subset G$ be a subset. We call $ H$ a subgroup of $ G$ if $ H$ is a group under the same operation as $ G$. That is, the operation on $ H$ is precisely the restriction $ \cdot |_{H \times H}$.

In particular, $ H$ must be closed under the operation of $ G$. For instance, the set of even integers $ 2\mathbb{Z}$ is a subset of the set of all integers $ \mathbb{Z}$, and the sum of any two even numbers is even, so this is a subgroup. Similarly, the subset of all integers which are multiples of $ n$ forms a subgroup of $ \mathbb{Z}$, and we denote it $ n\mathbb{Z}$. On the other hand, the subset of integers modulo $ n$ is not a subgroup of $ \mathbb{Z}$, because the operation is not just addition. As we will see in a bit, $ \mathbb{Z}/n\mathbb{Z}$ is a quotient of $ \mathbb{Z}$, justifying the unexplained division notation.

Another example is the subgroup of rotations within the group of symmetries of the regular $ n$-gon, and the subgroup of matrices with determinant 1 within the group of invertible matrices $ GL_n(\mathbb{R})$. The reader may easily verify that these are indeed subgroups.

We are about to give the most important example of subgroups, but first we must speak of homomorphisms.

Definition: Let $ G, H$ be two groups. A function $ \varphi: G \to H$ is called a homomorphism if $ \varphi(xy) = \varphi(x)\varphi(y)$ for all $ x,y \in G$.

Note that the operation on the left-hand side of the equality is happening with the operation in $ G$, but on the right-hand side it is happening in $ H$. In short, this condition says that the map $ \varphi$ preserves the structure of the group, at least in some coarse way.

We have already seen an example of a group homomorphism between the group $ \mathbb{Z}/4\mathbb{Z}$ and the subgroup of rotations of the square. There we said that $ \varphi(\rho^k) = k \mod 4$, and indeed

$$\varphi(\rho^n \rho^m) = \varphi(\rho^{n+m}) = n+m \mod 4 = (n \mod 4) + (m \mod 4)$$

So this is a group homomorphism. Here the homomorphism also happens to be a bijection. In this case we call it an isomorphism, but this need not always be the case. For example, if $ G$ is a group of invertible matrices under multiplication, the operation of taking a determinant is is group homomorphism to the multiplicative group of nonzero real numbers $ \textup{det}: GL_n(\mathbb{R}) \to \mathbb{R} – \left \{ 0 \right \}$. Indeed, $ \textup{det}(AB) = \textup{det}(A)\textup{det}(B)$ for all matrices $ A,B$. But many different matrices have equal determinants, so this map cannot be a bijection.

It is easy to verify (and we will leave it to the reader) that group homomorphisms always preserve the identity and inverses. For a slightly more detailed exercise, the reader can prove that the set-theoretic image of a homomorphism is a subgroup of the target group (you may want to use the “three properties” detailed below for this).

Now our important subgroup example is simply the set of things in a group homomorphism which get sent to the identity. That is:

Definition: The kernel of a group homomorphism $ \varphi: G \to H$, denoted $ \ker \varphi$ is the preimage of the identity $ \varphi^{-1}(1_H)$.

To verify that this is a group, let’s verify the three group properties (distributivity obviously holds since $ G$ is a group).

So the kernel of a homomorphism is a valid subgroup of $ G$.

Now something amazing happens with group homomorphisms. We just saw that the set of things which map to the identity form a group themselves, but there’s more to the story. As the reader knows, or can easily verify, every function $ f: G \to H$ between two sets induces an equivalence relation on $ G$, where two elements are equivalent if they get mapped to the same element in $ H$. For group homomorphisms we can say something much more powerful: the set of equivalence classes of a homomorphism forms a group. As we will see, the identity in this group is precisely the kernel of the homomorphism. This is a deep fact about groups, so let’s make it more rigorous.

Definition: Let $ G$ be a group, and let $ H$ be a subgroup. The left coset of $ H$ by an element $ x \in G$ is the set

$$xH = \left \{ xy: y \in H \right \}$$

Similarly, the right coset by $ x$ is $ Hx = \left \{ yx : y \in H \right \}$.

For example, one can take the trivial coset $ 1H$, and it is easy to verify that the coset $ hH = H$ if and only if $ h \in H$.

In general nonabelian groups the right coset and left coset if $ H$ by the same element will not agree. Moreover, as sets sometimes two left cosets $ xH, yH$ will be equal even when $ x \neq y$. In fact, they will be equal if and only if $ y^{-1}x \in H$. In particular, if $ xH = yH$, then there are two elements $ z, z’ \in H$ for which $ xz = yz’$, or equivalently $ y^{-1}x = z’z^{-1}$. But $ z, z’$ are both in $ H$, so these two products are.

Since set equality is an equivalence relation, we just defined an equivalence relation on $ G$ by $ x \sim y$ if $ y^{-1}x \in H$. The equivalence classes are just the cosets, and we can ask what is required for the set of equivalence classes to form a group. But before we do that, let’s verify what we said about group homomorphisms holds. That is, if $ x \ker \varphi = y \ker \varphi$, we have $ y^{-1}x \in \ker \varphi$, so that $ \varphi(y^{-1}x) = 1 = \varphi(y)^{-1} \varphi(x)$. In other words, $ \varphi(y) = \varphi(x)$, as we claimed.

Now here’s the cool part. We can “multiply” two cosets $ xHyH$ by calling this product $ \left \{ ab : a \in xH, b \in yH \right \}$. If we want the set of left cosets to form a group under this operation, we require the usual properties to hold:

Associativity will follow form closure, since it is just $ xyzH$ and the group operation in $ G$ is associative. Suppose that the identity part works and let’s look at closure: if $ xHyH = xyH = xyH1H$, then we can isolate the middle parts, and see that $ Hy = yH$ (the argument really should be more detailed, and we leave it to the reader to flush it out). That is, the left and right cosets by $ y$ must be equal!

Moreover, if left and right cosets are always equal, then one can easily verify that these properties all hold. So we just proved the following statement:

Theorem: The set of left (right) cosets of a subgroup $ H \subset G$ form a group if and only if the left and right cosets by $ x$ agree for any $ x \in G$.

And for the final stroke: left and right cosets agree for kernels. Let $ x \ker \varphi$ be such a coset; we want to show that for any $ z \in \ker \varphi$, we have $ xz = yx$ for some $ y \in \ker \varphi$. This is equivalent to requiring that $ xzx^{-1} \in \ker \varphi$, and indeed $ \varphi(xzx^{-1}) = \varphi(x)\varphi(z)\varphi(x)^{-1} = \varphi(x)\varphi(x)^{-1} = 1$. So the cosets of a kernel always form a group.

This condition that the left and right cosets agree (or that $ xzx^{-1} \in H$ for all $ z \in H, x \in G$) is such an important condition that we give it a name:

Definition: If the left and right cosets of a subgroup $ H \subset G$ agree, we call it a normal subgroup.

Now our theorem is simply: the cosets of a subgroup form a group if and only if the subgroup is normal, and kernels are always normal subgroups. To put the final touches on this mathematical cake, it just so happens that every normal subgroup is the kernel of some homomorphism. To see this, we just need one more definition.

Definition: Let $ G$ be a group and $ N$ be a normal subgroup. The quotient group of $ G$ by $ N$, denoted $ G/N$, is the group of left cosets of $ N$ in $ G$.

The important part is that there is an obvious group homomorphism $ G \to G/N$: just send an element $ x$ to the coset $ xN$. We call this map the canonical projection of $ G$ onto $ G/N$. Indeed it is surjective (hence the name projection), and the kernel of this homomorphism is clearly $ N$ (since $ xN = N$ if and only if $ x \in N$). So every normal subgroup is the kernel of the canonical projection map onto its quotient.

As a quick aside, the avid reader of this blog may recognize the notation and terminology form our post on constructing topological spaces. Indeed, the quotients introduced here are in a sense identical to quotients of groups, but in a different “setting.” The exploration of these analogous constructions in different settings falls under the name of category theory. Category theory happens to be extremely interesting and have a computational flavor; needless to say, we will be investigating it on this blog in the future.

The promised example here is of $ \mathbb{Z}/n\mathbb{Z}$. As we already saw, $ n\mathbb{Z}$ is a subgroup of $ \mathbb{Z}$, and it is normal simply because $ \mathbb{Z}$ is an abelian group (every subgroup of an abelian group is normal). So the cosets (denoted $ x + n\mathbb{Z}$ in the additive style) correspond to the remainders modulo $ n$: $ x + n\mathbb{Z} = y + n\mathbb{Z}$ if and only if $ y-z$ is a multiple of $ n$. The connection is immediate.

Lagrange’s Theorem

The language of quotients and cosets immediately gives us some powerful tools. The most immediate one is called Lagrange’s Theorem. In our discussion of cosets, we implicitly realized that the set of left cosets of $ H \subset G$ partition a $ G$ (every equivalence relation defines a partition). Moreover, it is interesting to note that all of these cosets have equal size!

To see this, note that for a fixed $ x \in G$ there is a natural bijection $ G \to G$ defined by left multiplication by $ x$. The nice thing about bijections is that they preserve the size of sets. So if we can restrict this map to a coset $ yH$ and the image is another coset $ zH$, then these two cosets have the same size.

Indeed, for any given $ y, z$, choose $ x = zy^{-1}$. Then left-multiplication by $ x$ gives $ zy^{-1}yH = zH$. As we mentioned in our discussion of cosets, this operation is well defined (in the sense that we chose the representative $ z$ of $ zH$ and ended up with the representative $ y$ of $ yH$). Since $ y,z$ were arbitrary, it must be the case that all left cosets have the same size.

Theorem: (Lagrange) Let $ G$ be a finite group. The order of any subgroup $ H \subset G$ divides the order of $ G$.

Proof. Note that $ H$ is a left coset of $ H$ (by, say, the identity). Further note that since $ G$ is finite, there are finitely many cosets of $ H$. Denote by $ [G:H]$ the number of cosets of $ H$ in $ G$. Since all cosets have the same size, they are disjoint, and the union of all cosets of $ H$ is $ G$, it must be that $ |H| [G:H] = |G|$. In particular, the order of $ H$ divides the order of $ G$. $ \square$

This imposes a very large amount of structure on a group. For instance, one can now say that a group of primer order $ p$ has no nontrivial subgroups except for the whole group itself (indeed, with a little more work we can completely characterize groups of prime order). Further, any group of order $ 2^n$ cannot have subgroups of odd order (except the identity subgroup). Many of the arguments of group theory turn into arguments by divisibility solely because of this theorem. And the proof is essentially summed up by the phrase “multiplication by a group element is bijective.” This is a gem of elegance that shows the power of viewing mathematics from the perspective of functions.

It is common to call the quantity $ [G:H]$ in the proof above the index of $ H$ in $ G$. As we said, this is nothing more than the number of cosets of $ H$, and it satisfies $ |G| = [G:H] |H|$.

Group Actions

The last thing we will discuss in this primer is the idea of a group action. As we mentioned, the important part about group theory is that groups represent symmetries of things. Going back to our example of a square, it’s not that a square itself is a group in a nice way, but that the symmetries of a square form a group. This is an important distinction, because we are saying that somehow the symmetry group of the square “performs an action” on the square.

This gives us a hint that we should define what it means for a general group to “perform actions” on a general set.

Definition: A group $ G$ acts on a set $ A$ if there is a group homomorphism $ \varphi: G \to S(A)$, where $ S(A)$ is the group of bijections $ A \to A$. We call $ \varphi$ a group action.

Let’s dissect this definition a little. What we’re saying is that we want to associate elements of $ G$ with operations on $ A$. If $ g \in G$ and $ a \in A$, then $ \varphi(g): A \to A$ permutes the elements of $ A$ in some way. We can even go so far as to identify $ g$ with its image in $ S(A)$, and write $ ga$ for the action of (the function) $ g$ on (the set element) $ a$.

For example, $ \mathbb{Z}/4\mathbb{Z}$ acts on the square by sending $ n \mapsto \rho^n$, where $ \rho$ is again the quarter turn rotation. Indeed, any finite symmetry group $ S_n$ acts on the set of numbers $ 1, \dots, n$ by permutations (this is how they were defined), and for general sets $ A$, the group $ S(A)$ acts on $ A$ (the homomorphism is the identity map). Specific examples we’ve seen on this blog include matrix groups acting on vector spaces and homeomorphisms acting on topological spaces.

There are a few important aspects of group actions that we will investigate in future posts. But at least for now we can prove a nice theorem using group actions:

Theorem: Every group is a subgroup of a group of symmetries. In particular, every finite group $ G$ is isomorphic to a subgroup of $ S_n$ for some $ n$.

Proof. Every group $ G$ acts on itself by left multiplication. That is, every element $ g \in G$ corresponds to a distinct isomorphism $ G \to G$ by sending $ x \mapsto gx$. Indeed, left multiplication by an element $ g$ is easily proven to be an isomorphism on $ G$. Furthermore, if $ g \neq h$ then $ g^{-1}h \neq 1$ and so left multiplication by $ h$ followed by left multiplication by $ g^{-1}$ is not the identity map on $ G$. This proves that two distinct elements in $ G$ correspond to two distinct isomorphisms of $ G$. That is, the group action is injective as a homomorphism $ G \to S(G)$. In general every injective map is a bijection onto its image, and the image of a homomorphism is always a subgroup. So the group action provides an isomorphism $ G \to \varphi(G) \subset S(G)$, as required. $ \square$

There is a whole host of things we have yet to talk about with groups. We will leave these for next time, but just to lay them on the table, we need to discuss:

That being said, group theory is a very large subject, and the reader may wish to pick up some books. This author learned algebra from two primary textual sources, the first being Michael Artin’s “Algebra” and the second (from a more mature perspective) being Paolo Aluffi’s “Algebra: Chapter 0”. We highly recommend the second text as a way to simultaneously learn algebra, demistify category theory, and see a wide host of applications of abstract algebra to other fields of mathematics.

Until next time!

Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.

DOI: https://doi.org/10.59350/nswbz-9kc20