There has been a lot of news recently on government surveillance of its citizens. The biggest two that have pervaded my news feeds are the protests in Turkey, which in particular have resulted in particular oppression of social media users, and the recent light on the US National Security Agency’s widespread “backdoor” in industry databases at Google, Verizon, Facebook, and others. It appears that the facts are in flux, as some companies have denied their involvement in this program, but regardless of the truth the eye of the public has landed firmly on questions of privacy.
Barack Obama weighed in on the controversy as well, being quoted as saying,
You can’t have 100% security and 100% privacy, and also zero inconvenience.
I don’t know what balance the US government hopes to strike, but what I do know is that privacy and convenience are technologically possible, and we need not relinquish security to attain it.
Before I elaborate, let me get my personal beliefs out of the way. I consider the threat of terrorism low compared to the hundreds of other ways I can die. I should know, as I personally have been within an $ \varepsilon$ fraction of my life for all $ \varepsilon > 0$ (when I was seven I was hit by a bus, proclaimed dead, and revived). So I take traffic security much more seriously than terrorism, and the usual statistics will back me up in claiming one would be irrational to do otherwise. On the other hand, I also believe that I only need so much privacy. So I don’t mind making much of my personal information public, and I opt in to every one of Google’s tracking services in the hopes that my user experience can be improved. Indeed it has, as services like Google Now will, e.g., track my favorite bands for me based on my Google Play listening and purchasing habits, and alert me when there are concerts in my area. If only it could go one step further and alert me of trending topics in theoretical computer science! I have much more utility for timely knowledge of these sorts of things than I do for the privacy of my Facebook posts. Of course, ideologically I’m against violating privacy as a matter of policy, but this is a different matter. One can personally loathe a specific genre of music and still recognize its value and one’s right to enjoy it.
But putting my personal beliefs aside, I want to make it clear that there is no technological barrier to maintaining privacy and utility. This may sound shocking, but it rings true to the theoretical computer scientist. Researchers in cryptography have experienced this feeling many times, that their wildest cryptographic dreams are not only possible but feasible! Public-key encryption and digital signatures, secret sharing on a public channel, zero-knowledge verification, and many other protocols have been realized quite soon after being imagined. There are still some engineering barriers to implementing these technologies efficiently in large-scale systems, but with demand and a few years of focused work there is nothing stopping them from being used by the public. I want to use this short post to describe two of the more recent ideas that have pervaded the crypto community and provide references for further reading.
Differential Privacy and Fully Homomorphic Encryption
There are two facts which are well known in theoretical computer science that the general public is not aware of. The first is about the privacy of databases:
There is a way to mine information from a database without the ability to inspect individual entries in the database.
This is known as differential privacy. The second is no less magical:
There are secure encryption schemes which allow one to run programs on encrypted data and produce encrypted results, without the ability to decrypt the data.
This is known as fully homomorphic encryption.
The implications of these two facts should be obvious: search engines need not know our queries but can still fetch us search results and mine our information to serve ads, Facebook need not have access to our personal data but may still accurately predict new friends, grocery stores can even know what products to place side by side without knowing what any individual customer has purchased. Banks could process our transactions without knowing the amounts involved, or even the parties involved. Perhaps most importantly, governments can have access to databases (in the form of differentially private queries) and mine for the existence of threats without violating any individual user’s privacy. If they get an indication of a terrorist threat, then they can use the usual channels (court orders) to get access to specific individual data.
It’s easy to argue that these techniques will never become mainstream enough for individuals to benefit from it. Indeed, we’ve had cryptography for many years but few average users actively encrypt their communication for a lack of convenience. And then there are questions of policy: why would any company relinquish the ability to work directly with user data? And the cost of rearchitecturing existing services to utilize these technologies would be enough to dissuade most business leaders.
But the point of all this is that these are problems of policy that could in principle be solved without waiting for governments and corporations to get their act together. With enough demand for such services and with enough technologically-minded entrepreneurs (I’m looking at you, Silicon Valley), it would be just a matter of time before the world was differentially private. Mathematics cannot be revoked or legislated away.
Fully Homomorphic Encryption
A fully homomorphic encryption scheme is a normal encryption scheme (two functions “enc” and “dec” to encrypt and decrypt) with one additional function, which we’ll call “eval.” Very roughly, eval accepts as input the text of a program and a ciphertext, and produces as output a ciphertext such that the following diagram commutes:
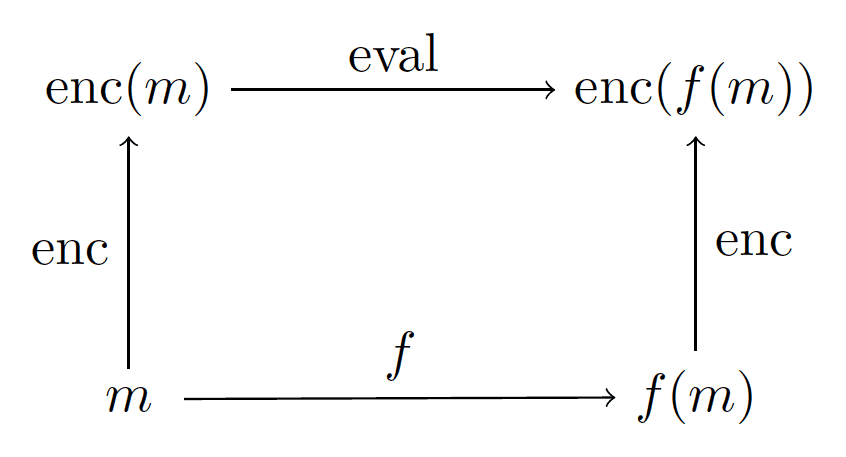
FHE-diagram
That is, $ m$ is our message, and $ \textup{eval}$ runs $ f$ on the encrypted version of our message. In practice this happens by lifting two operations, multiplication and addition, from plaintexts (which are usually number-representations of letters) to ciphertexts (again usually numbers). Once this is done one can simulate the functionality of an arbitrary circuit on the encrypted data without decrypting it. Those readers who have been following our category theory series will recognize these sorts of diagrams as being functorial. [Actually, at the time of this writing we have yet to look at functors, but we will soon!] So perhaps a better term would be “functorial encryption.”
I should emphasize: a truly homomorphic encryption scheme has the ability to run any computable function on the encrypted data. There is no loss of functionality in preserving the privacy from the program runner. The main use of this is to maintain privacy while deferring large computations to the cloud. We do this all the time, e.g. a search query, but it also applies to big websites like Reddit, which operate entirely on Amazon Web Services.
Fully homomorphic encryption was first envisaged by Rivest, Adleman (two of the inventors of RSA), and Dertouzos in the late seventies, mainly because the RSA encryption scheme is close to being homomorphic (one can multiply ciphertexts, but not add them). In 2009, Craig Gentry released the first working fully-homomorphic scheme based on the mathematical theory of ideal lattices, and later that year he (with a group of other researchers) came up with a second system that is arguably as simple as RSA; it operates on integers with modular arithmetic.
Gentry has produced a lot of research since then in homomorphic encryption, but the interested reader should probably start with his tutorial paper describing his arithmetic-based system. From there, there are existing implementations in Python (using Sage) and C++, both of which are freely available on github.
Differential Privacy
The main idea of differential privacy is that one can add noise to statistical data to protect the identities of individual records. Slightly more rigorously, a randomized algorithm $ f$ is said to be $ \varepsilon$-differentially private if for all possible datasets (inputs) $ D_1, D_2$ which differ on a single record, and all possible collections of outputs $ y$ of $ f$, the probability of correctly guessing $ D_1$ from $ y$ is not significantly different from that of $ D_2$. In particular, their quotient is at most $ e^{\varepsilon}$ (this choice of using $ e$ is arbitrary, but makes the analysis nicer).
The motivation for differential privacy came from two notable events in which companies released “anonymized” data which was partially de-anonymized because it was too specific. The first was the million-dollar Netflix Prize contest to develop a better recommendation algorithm, and the second was the release of the Massachusetts Group Insurance Commission medical database. As such, many companies are very strict with how they handle their user data, and information sharing the medical community is practically nonexistent.
There are many known differentially private algorithms, and they’re much stronger than one would imagine at first. One can run random forests of decision trees, network trace analysis, certain forms of clustering, and a whole host of combinatorial optimization problems. For a gentle introduction to differential privacy, see Christine Task’s lecture video, a Practical Beginner’s Guide to Differential Privacy. There is also an influential survey from Microsoft Research of Dwork. These go into much more detail about the abilities and inabilities of differential privacy than I could do here.
If there’s one thing to take away from this discussion, it’s that efficient protocols for ensuring privacy are out there waiting to be implemented in software. So while we complain and listen to others complain about governments violating our liberties (and indeed, this discussion is extremely important to have), let’s do a little mathematics, do a little computer science, and figure out how to make privacy the standard of measure in software.
Until next time!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.