This post is intended for people with a little bit of programming experience and no prior mathematical background.
So let’s talk about numbers.
Numbers are curious things. On one hand, they represent one of the most natural things known to humans, which is quantity. It’s so natural to humans that even newborn babies are in tune with the difference between quantities of objects between 1 and 3, in that they notice when quantity changes much more vividly than other features like color or shape.
But our familiarity with quantity doesn’t change the fact that numbers themselves (as an idea) are a human invention. And they’re not like most human inventions, the kinds where you have to tinker with gears or circuits to get a machine that makes your cappuccino. No, these are mathematical inventions. These inventions exist only in our minds.
Numbers didn’t always exist. A long time ago, back when the Greeks philosophers were doing their philosophizing, negative numbers didn’t exist! In fact, it wasn’t until 1200 AD that the number zero was first considered in Europe. Zero, along with negative numbers and fractions and square roots and all the rest, were invented primarily to help people solve more problems than they could with the numbers they had available. That is, numbers were invented primarily as a way for people to describe their ideas in a useful way. People simply wondered “is there a number whose square gives you 2?” And after a while they just decided there was and called it $ \sqrt{2}$ because they didn’t have a better name for it.
But with these new solutions came a host of new problems. You see, although I said mathematical inventions only exist in our minds, once they’re invented they gain a life of their own. You start to notice patterns in your mathematical objects and you have to figure out why they do the things they do. And numbers are a perfectly good example of this: once I notice that I can multiply a number by itself, I can ask how often these “perfect squares” occur. That is, what’s the pattern in the numbers $ 1^2, 2^2, 3^2, 4^2, \dots$? If you think about it for a while, you’ll find that square numbers have a very special relationship with odd numbers.
Other times, however, the things you invent turn out to make no sense at all, and you can prove they never existed in the first place! It’s an odd state of affairs, but we’re going to approach the subject of complex numbers from this mindset. We’re going to come up with a simple idea, the idea that negative numbers can be perfect squares, and explore the world of patterns it opens up. Along the way we’ll do a little bit of programming to help explore, give some simple proofs to solidify our intuition, and by the end we’ll see how these ideas can cause wonderful patterns like this one:

mandelbrot
The number i
Let’s bring the story back around to squares. One fact we all remember about numbers is that squaring a number gives you something non-negative. $ 7^2 = 49, (-2)^2 = 4, 0^2 = 0$, and so on. But it certainly doesn’t have to be this way. What if we got sick of that stupid fact and decided to invent a new number whose square was negative? Which negative, you ask? Well it doesn’t really matter, because I can always stretch it larger or smaller so that it’s square is -1.
Let’s see how: if you say that your made-up number $ x$ makes $ x^2 = -7$, then I can just use $ \frac{x}{\sqrt{7}}$ to get a number whose square is -1. If you’re going to invent a number that’s supposed to interact with our usual numbers, then you have to be allowed to add, subtract, and multiply $ x$ with regular old real numbers, and the usual properties would have to still work. So it would have to be true that $ (x / \sqrt{7})^2 = x^2 / \sqrt{7}^2 = -7/7 = -1$.
So because it makes no difference (this is what mathematicians mean by, “without loss of generality”) we can assume that the number we’re inventing will have a square of negative one. Just to line up with history, let’s call the new number $ i$. So there it is: $ i$ exists and $ i^2 = -1$. And now that we are “asserting” that $ i$ plays nicely with real numbers, we get these natural rules for adding and subtracting and multiplying and dividing. For example
- $ 1 + i$ is a new number, which we’ll just call $ 1+i$. And if we added two of these together, $ (1+ i) + (1+i)$, we can combine the real parts and the $ i$ parts to get $ 2 + 2i$. Same goes for subtraction. In general a complex number looks like $ a + bi$, because as we’ll see in the other points you can simplify every simple arithmetic expression down to just one “real number” part and one “real number times $ i$” part.
- We can multiply $ 3 \cdot i$, and we’ll just call it $ 3i$, and we require that multiplication distributes across addition (that the FOIL rule works). So that, for example, $ (2 – i)(1 + 3i) = (2 + 6i – i – 3i^2) = (2 + 3) + (6i – i) = (5 + 5i)$.
- Dividing is a significantly more annoying. Say we want to figure out what $ 1 / (1+i)$ is (in fact, it’s not even obvious that this should look like a regular number! But it does). The $ 1 / a$ notation just means we’re looking for a number which, when we multiply by the denominator $ a$, we get back to 1. So we’re looking to find out when $ (a + bi)(1 + i) = 1 + 0i$ where $ a$ and $ b$ are variables we’re trying to solve for. If we multiply it out we get $ (a-b) + (a + b)i = 1 + 0i$, and since the real part and the $ i$ part have to match up, we know that $ a – b = 1$ and $ a + b = 0$. If we solve these two equations, we find that $ a = 1/2, b = -1/2$ works great. If we want to figure out something like $ (2 + 3i) / (1 – i)$, we just find out what $ 1 / (1- i)$ is first, and then multiply the result by $ (2+3i)$.
So that was tedious and extremely boring, and we imagine you didn’t even read it (that’s okay, it really is boring!). All we’re doing is establishing ground rules for the game, so if you come across some arithmetic that doesn’t make sense, you can refer back to this list to see what’s going on. And once again, for the purpose of this post, we’re asserting that all these laws hold. Maybe some laws follow from others, but as long as we don’t come up with any nasty self-contradictions we’ll be fine.
And now we turn to the real questions: is $ i$ the only square root of -1? Does $ i$ itself have a square root? If it didn’t, we’d be back to where we started, with some numbers (the non-$ i$ numbers) having square roots while others don’t. And so we’d feel the need to make all the $ i$ numbers happy by making up more numbers to be their square roots, and then worrying what if these new numbers don’t have square roots and…gah!
I’ll just let you in on the secret to save us from this crisis. It turns out that $ i$ does have a square root in terms of other $ i$ numbers, but in order to find it we’ll need to understand $ i$ from a different angle, and that angle turns out to be geometry.
Geometry? How is geometry going to help me understand numbers!?
It’s a valid question and part of why complex numbers are so fascinating. And I don’t mean geometry like triangles and circles and parallel lines (though there will be much talk of angles), I mean transformations in the sense that we’ll be “stretching,” “squishing,” and “rotating” numbers. Maybe another time I can tell you why for me “geometry” means stretching and rotating; it’s a long but very fun story.
The clever insight is that you can represent complex numbers as geometric objects in the first place. To do it, you just think of $ a + bi$ as a pair of numbers $ (a,b)$, (the pair of real part and $ i$ part), and then plot that point on a plane. For us, the $ x$-axis will be the “real” axis, and the $ y$-axis will be the $ i$-axis. So the number $ (3 – 4i)$ is plotted 3 units in the positive $ x$ direction and 4 units in the negative $ y$ direction. Like this:
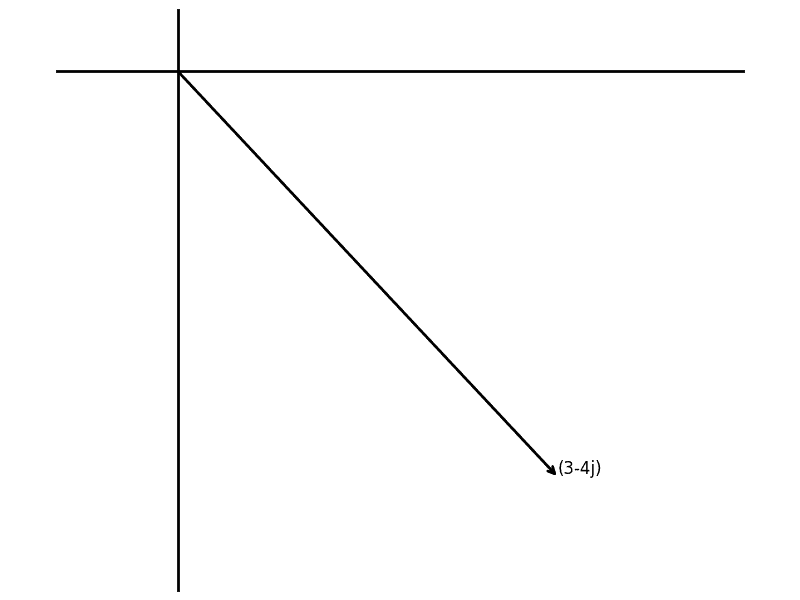
single-complex-number
We draw it as an arrow for a good reason. Stretching, squishing, rotating, and reflecting will all be applied to the arrow, keeping its tail fixed at the center of the axes. Sometimes the arrow is called a “vector,” but we won’t use that word because here it’s synonymous with “complex number.”
So let’s get started squishing stuff.
Stretching, Squishing, Rotating
Before we continue I should clear up some names. We call a number that has an $ i$ in it a complex number, and we call the part without the $ i$ the real part (like 2 in $ 2-i$) and the part with $ i$ the complex part.
Python is going to be a great asset for us in exploring complex numbers, so let’s jump right into it. It turns out that Python natively supports complex numbers, and I wrote a program for drawing complex numbers. I used it to make the plot above. The program depends on a library I hate called matplotlib, and so the point of the program is to shield you from as much pain as possible and focus on complex numbers. You can use the program by downloading it from this blog’s Github page, along with everything else I made in writing this post. All you need to know how to do is call a function.
Here’s the function header:
# plotComplexNumbers : [complex] -> None
# display a plot of the given list of complex numbers
def plotComplexNumbers(numbers):
...
Before we show some examples of how to use it, we have to understand how to use complex numbers in Python. It’s pretty simple, except that Python was written by people who hate math, and so they decided the complex number would be represented by $ j$ instead of $ i$ (people who hate math are sometimes called “engineers,” and they use $ j$ out of spite. Not really, though).
So in Python it’s just like any other computation. For example:
>>> (1 + 1j)*(4 - 2j) == (6+2j)
True
>>> 1 / (1+1j)
(0.5-0.5j)
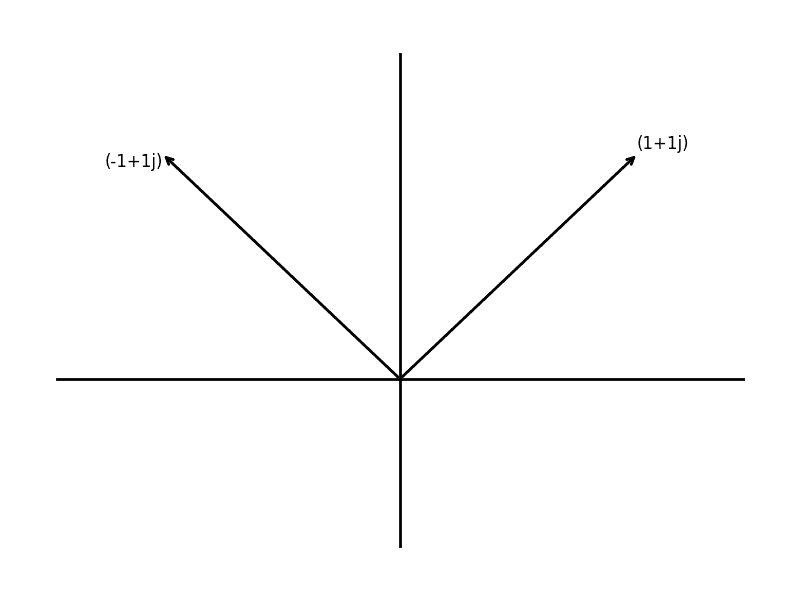
And so calling the plotting function with a given list of complex numbers is as simple as importing the module and calling the function
from plotcomplex import plot
plot.plotComplexNumbers([(-1+1j), (1+2j), (-1.5 - 0.5j), (.6 - 1.8j)])
Here’s the result
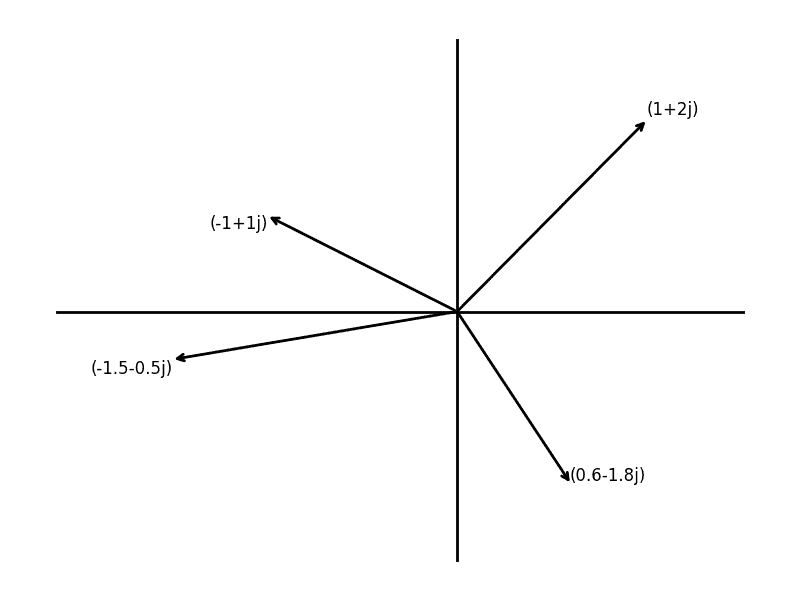
example-complex-plot
So let’s use plots like this one to explore what “multiplication by $ i$” does to a complex number. It might not seem exciting at first, but I promise there’s a neat punchline.
Even without plotting it’s pretty easy to tell what multiplying by $ i$ does to some numbers. It takes 1 to $ i$, moves $ i$ to $ i^2 = -1$, it takes -1 to $ -i$, and $ -i$ to $ -i \cdot i = 1$.
What’s the pattern in these? well if we plot all these numbers, they’re all at right angles in counter-clockwise order. So this might suggest that multiplication by $ i$ does some kind of rotation. Is that always the case? Well lets try it with some other more complicated numbers. Click the plots below to enlarge.
Well, it looks close but it’s hard to tell. Some of the axes are squished and stretched, so it might be that our images don’t accurately represent the numbers (the real world can be such a pain). Well when visual techniques fail, we can attempt to prove it.
Clearly multiplying by $ i$ does some kind of rotation, maybe with other stuff too, and it shouldn’t be so hard to see that multiplying by $ i$ does the same thing no matter which number you use (okay, the skeptical readers will say that’s totally hard to see, but we’ll prove it super rigorously in a minute). So if we take any number and multiply it by $ i$ once, then twice, then three times, then four, and if we only get back to where we started at four multiplications, then each rotation had to be a quarter turn.
Indeed,
$$\displaystyle (a + bi) i^4 = (ai – b) i^3 = (-a – bi) i^2 = (-ai + b) i = a + bi$$This still isn’t all that convincing, and we want to be 100% sure we’re right. What we really need is a way to arithmetically compute the angle between two complex numbers in their plotted forms. What we’ll do is find a way to measure the angle of one complex number with the $ x$-axis, and then by subtraction we can get angles between arbitrary points. For example, in the figure below $ \theta = \theta_1 – \theta_2$.
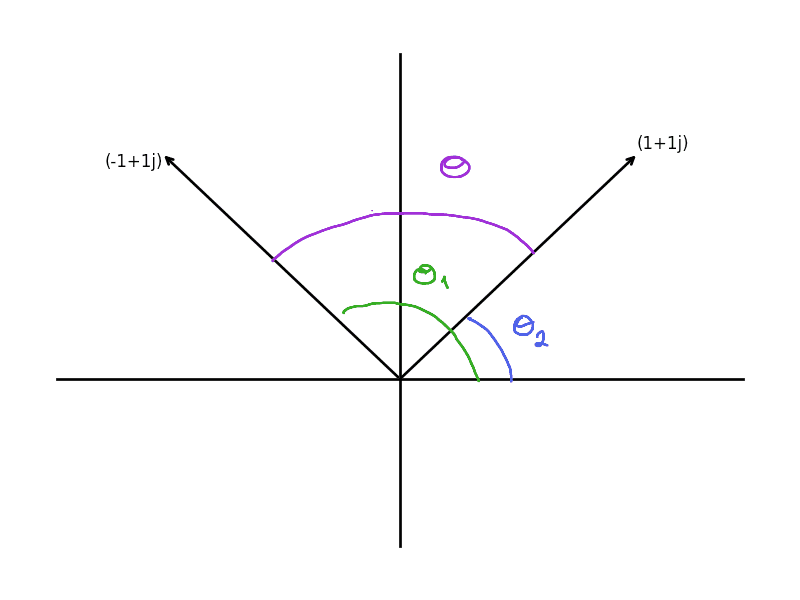
angle-example
One way to do this is with trigonometry: the geometric drawing of $ a + bi$ is the hypotenuse of a right triangle with the $ x$-axis.
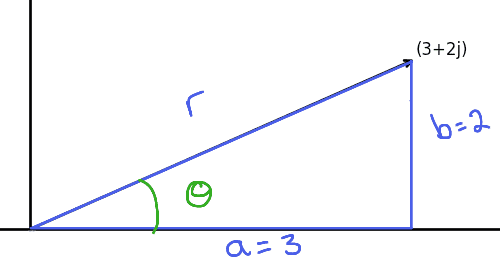
triangle-example
And so if $ r$ is the length of the arrow, then by the definition of sine and cosine, $ \cos(\theta) = a/r, \sin(\theta) = b/r$. If we have $ r, \theta$, and $ r > 0$, we can solve for a unique $ a$ and $ b$, so instead of representing a complex number in terms of the pair of numbers $ (a,b)$, we can represent it with the pair of numbers $ (r, \theta)$. And the conversion between the two is just
$$a + bi = r \cos(\theta) + (r \sin(\theta)) i$$The $ (r, \theta)$ representation is called the polar representation, while the $ (a,b)$ representation is called the rectangular representation or the Cartesian representation. Converting between polar and Cartesian coordinates fills the pages of many awful pre-calculus textbooks (despite the fact that complex numbers don’t exist in classical calculus). Luckily for us Python has built-in functions to convert between the two representations for us.
>>> import cmath
>>> cmath.polar(1 + 1j)
(1.4142135623730951, 0.7853981633974483)
>>> z = cmath.polar(1 + 1j)
>>> cmath.rect(z[0], z[1])
(1.0000000000000002+1j)
It’s a little bit inaccurate on the rounding, but it’s fine for our purposes.
So how do we compute the angle between two complex numbers? Just convert each to the polar form, and subtract the second coordinates. So if we get back to our true goal, to figure out what multiplication by $ i$ does, we can just do everything in polar form. Here’s a program that computes the angle between two complex numbers.
def angleBetween(z, w):
zPolar, wPolar = cmath.polar(z), cmath.polar(w)
return wPolar[1] - zPolar[1]
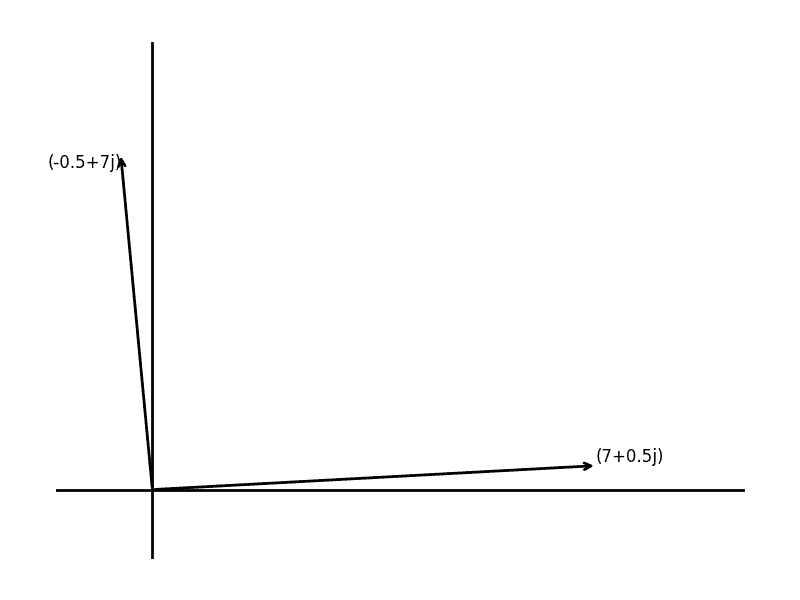
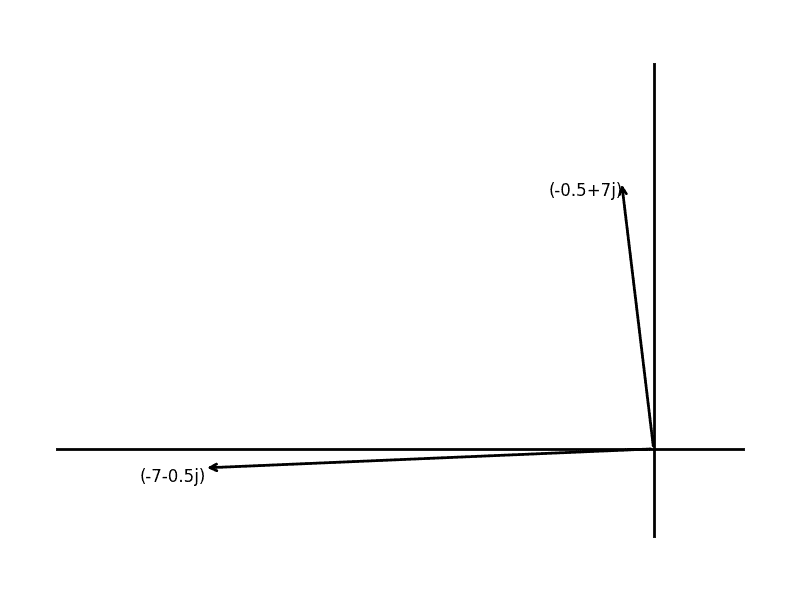
print(angleBetween(1 + 1j, (1 + 1j) * 1j))
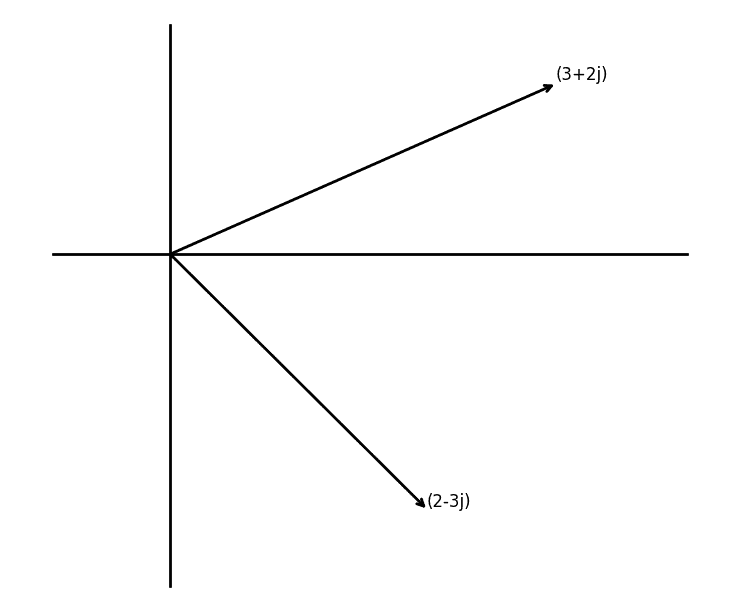
print(angleBetween(2 - 3j, (2 - 3j) * 1j))
print(angleBetween(-0.5 + 7j, (-0.5 + 7j) * 1j))
Running it gives
1.5707963267948966
1.5707963267948966
-4.71238898038469
Note that the decimal form of $ \pi/2$ is 1.57079…, and that the negative angle is equivalent to $ \pi/2$ if you add a full turn of $ 2\pi$ to it. So programmatically we can see that for every input we try multiplying by $ i$ rotates 90 degrees.
But we still haven’t proved it works. So let’s do that now. To say what the angle is between $ r \cos (\theta) + ri \sin (\theta)$ and $ i \cdot [r \cos (\theta) + ri \sin(\theta)] = -r \sin (\theta) + ri \cos(\theta)$, we need to transform the second number into the usual polar form (where the $ i$ is on the sine part and not the cosine part). But we know, or I’m telling you now, this nice fact about sine and cosine:
$ \displaystyle \sin(\theta + \pi/2) = cos(\theta)$
$$\displaystyle \cos(\theta + \pi / 2) = -\sin(\theta)$$This fact is maybe awkward to write out algebraically, but it’s just saying that if you shift the whole sine curve a little bit you get the cosine curve, and if you keep shifting it you get the opposite of the sine curve (and if you kept shifting it even more you’d eventually get back to the sine curve; they’re called periodic for this reason).
So immediately we can rewrite the second number as $ r \cos(\theta + \pi/2) + i r \sin (\theta + \pi/2)$. The angle is the same as the original angle plus a right angle of $ \pi/2$. Neat!
Applying this same idea to $ (a + bi) \cdot (c + di)$, it’s not much harder to prove that multiplying two complex numbers in general multiplies their lengths and adds their angles. So if a complex number $ z$ has its magnitude $ r$ smaller than 1, multiplying by $ z$ squishes and rotates whatever is being multiplied. And if the magnitude is greater than 1, it stretches and rotates. So we have a super simple geometric understanding of how arithmetic with complex numbers works. And as we’re about to see, all this stretching and rotating results in some really weird (and beautifully mysterious!) mathematics and programs.
But before we do that we still have one question to address, the question that started this whole geometric train of thought: does $ i$ have a square root? Indeed, I’m just looking for a number such that, when I square its length and double its angle, I get $ i = \cos(\pi/2) + i \sin(\pi/2)$. Indeed, the angle we want is $ \pi/4$, and the length we want is $ r = 1$, which means $ \sqrt{i} = \cos(\pi/4) + i \sin(\pi/4)$. Sweet! There is another root if you play with the signs, see if you can figure it out.
In fact it’s a very deeper and more beautiful theorem (“theorem” means “really important fact”) called the fundamental theorem of algebra. And essentially it says that the complex numbers are complete. That is, we can always find square roots, cube roots, or anything roots of numbers involving $ i$. It actually says a lot more, but it’s easier to appreciate the rest of it after you do more math than we’re going to do in this post.
On to pretty patterns!
The Fractal
So here’s a little experiment. Since every point in the plane is the end of some arrow representing a complex number, we can imagine transforming the entire complex plane by transforming each number by the same rule. The most interesting simple rule we can think of: squaring! So though it might strain your capacity for imagination, try to visualize the idea like this. Squaring a complex number is the same as squaring it’s length and doubling its angle. So imagine: any numbers whose arrows are longer than 1 will grow much bigger, arrows shorter than 1 will shrink, and arrows of length exactly one will stay the same length (arrows close to length 1 will grow/shrink much more slowly than those far away from 1). And complex numbers with small positive angles will increase their angle, but only a bit, while larger angles will grow faster.
Here’s an animation made by Douglas Arnold showing what happens to the set of complex numbers $ a + bi$ with $ 0 \leq a, b \leq 1$ or $ -1 < a,b < 0$. Again, imagine every point is the end of a different arrow for the corresponding complex number. The animation is for a single squaring, and the points move along the arc they would travel if one rotated/stretched them smoothly.
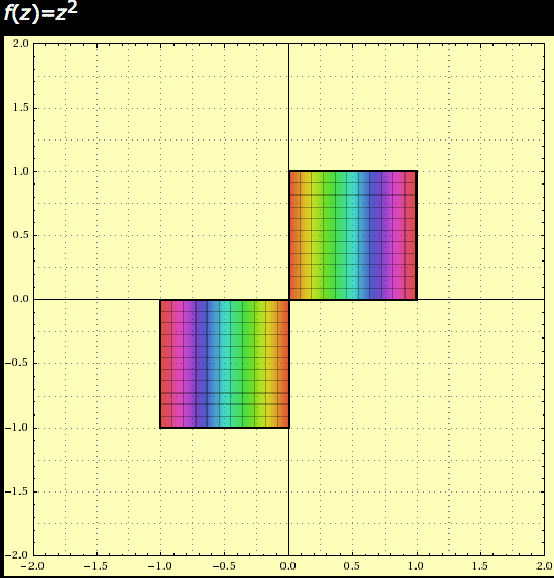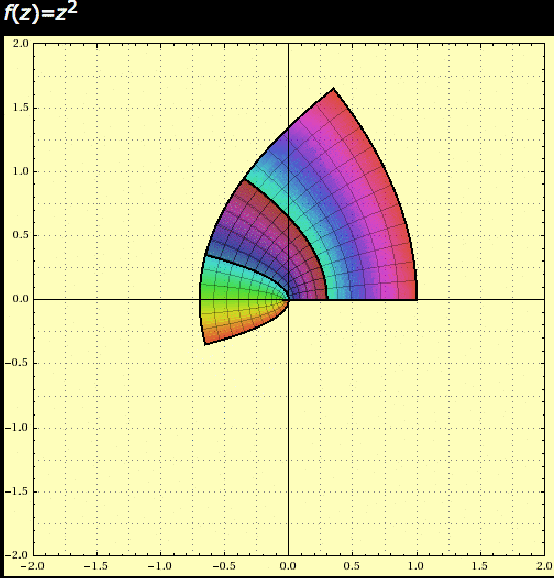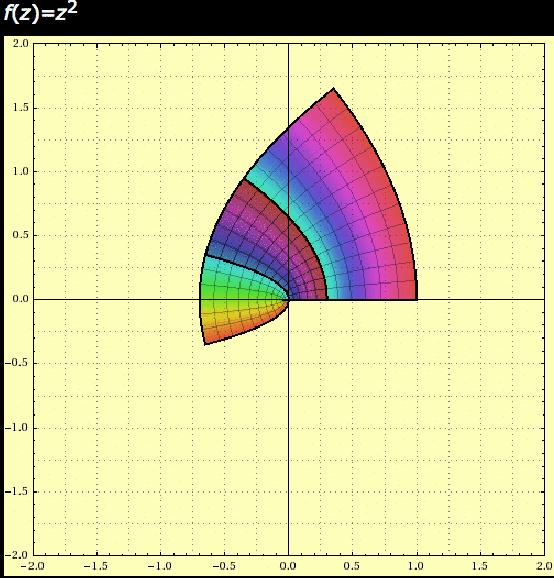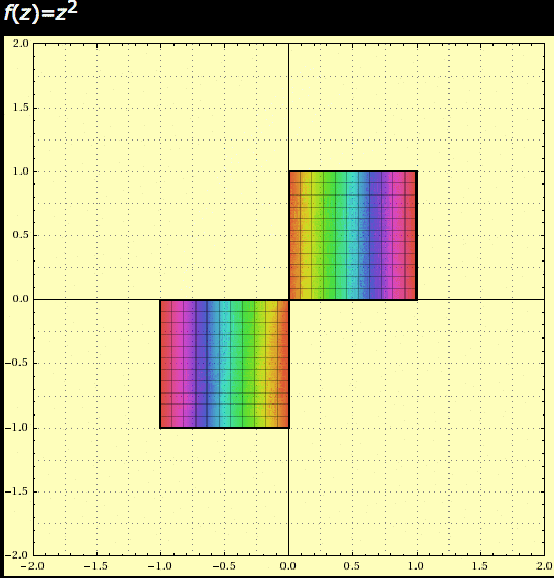
complex-squaring
So that’s pretty, but this is by all accounts a well-behaved transformation. It’s “predictable,” because for example we can always tell which complex numbers will get bigger and bigger (in length) and which will get smaller.
What if, just for the sake of tinkering, we changed the transformation a little bit? That is, instead of sending $ z = a+bi$ to $ z^2$ (I’ll often write this $ z \mapsto z^2$), what if we sent
$$\displaystyle z \mapsto z^2 + 1$$Now it’s not so obvious: which numbers will grow and which will shrink? Notice that it’s odd because adding 1 only changes the real part of the number. So a number whose length is greater than 1 can become small under this transformation. For example, $ i$ is sent to $ 0$, so something slightly larger would also be close to zero. Indeed, $ 5i/4 \mapsto -9/16$.
So here’s an interesting question: are there any complex numbers that will stay small even if I keep transforming like this forever? Specifically, if I call $ f(z) = z^2$, and I call $ f^2(z) = f(f(z))$, and likewise call $ f^k(z)$ for $ k$ repeated transformations of $ z$, is there a number $ z$ so that for every $ k$, the value $ f^k(z) < 2$? “Obvious” choices like $ z=0$ don’t work, and neither do random guesses like $ z=i$ or $ z=1$. So should we guess the answer is no?
Before we jump to conclusions let’s write a program to see what happens for more than our random guesses. The program is simple: we’ll define the “square plus one” function, and then repeatedly apply that function to a number for some long number of times (say, 250 times). If the length of the number stays under 2 after so many tries, we’ll call it “small forever,” and otherwise we’ll call it “not small forever.”
def squarePlusOne(z):
return z*z + 1
def isSmallForever(z, f):
k = 0
while abs(z) < 2: z = f(z) k += 1 if k > 250:
return True
return False
This isSmallForever function is generic: you can give it any function $ f$ and it will repeatedly call $ f$ on $ z$ until the result grows bigger than 2 in length. Note that the abs function is a built-in Python function for computing the length of a complex number.
Then I wrote a classify function, which you can give a window and a small increment, and it will produce a grid of zeros and ones marking the results of isSmallForever. The details of the function are not that important. I also wrote a function that turns the grid into a picture. So here’s an example of how we’d use it:
from plotcomplex.plot import gridToImage
def classifySquarePlusOne(z):
return isSmallForever(z, squarePlusOne)
grid = classify(classifySquarePlusOne) # the other arguments are defaulted to [-2,2], [-2,2], 0.1
gridToImage(grid)
And here’s the result. Points colored black grow beyond 2, and white points stay small for the whole test.
Looks like they'll always grow big.
So it looks like repeated squaring plus one will always make complex numbers grow big. That’s not too exciting, but we can always make it more exciting. What happens if we replace the 1 in $ z^2 + 1$ with a different complex number? For example, if we do $ z^2 – 1$ then will things always grow big?
You can randomly guess and see that 0 will never grow big, because $ 0^2 – 1 = -1$ and $ (-1)^2 – 1 = 0$. It will just oscillate forever. So with -1 some numbers will grow and some will not! Let’s use the same routine above to see which:
def classifySquareMinusOne(z):
return isSmallForever(z, squareMinusOne)
grid = classify(classifySquareMinusOne)
gridToImage(grid)
And the result:
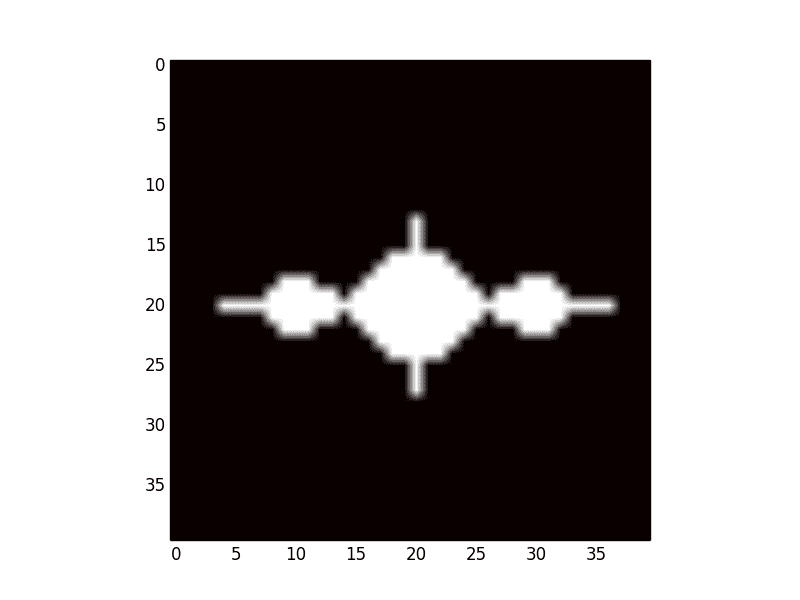
second-attempt
Now that’s a more interesting picture! Let’s ramp up the resolution
grid = classify(classifySquareMinusOne, step=0.001)
gridToImage(grid)
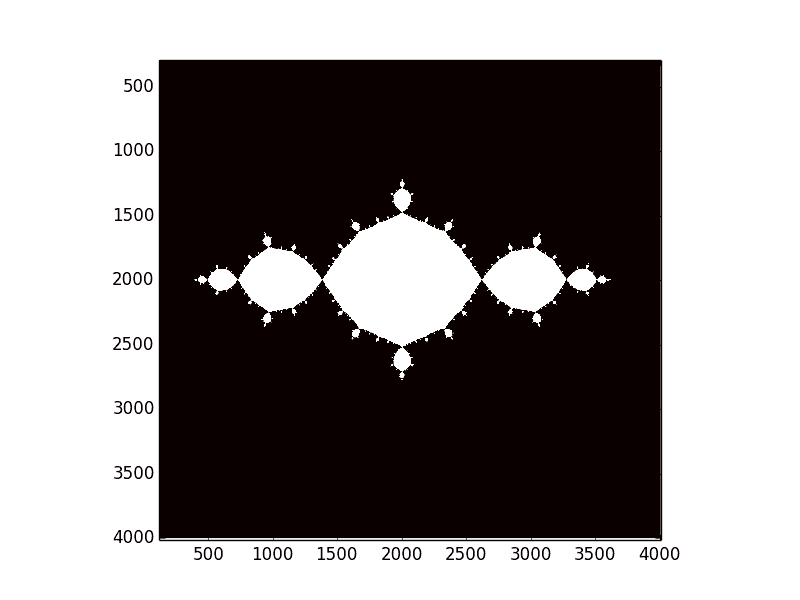
second-attempt-zoomed
Gorgeous. If you try this at home you’ll notice, however, that this took a hell of a long time to run. Speeding up our programs is very possible, but it’s a long story for another time. For now we can just be patient.
Indeed, this image has a ton of interesting details! It looks almost circular in the middle, but if we zoom in we can see that it’s more like a rippling wave
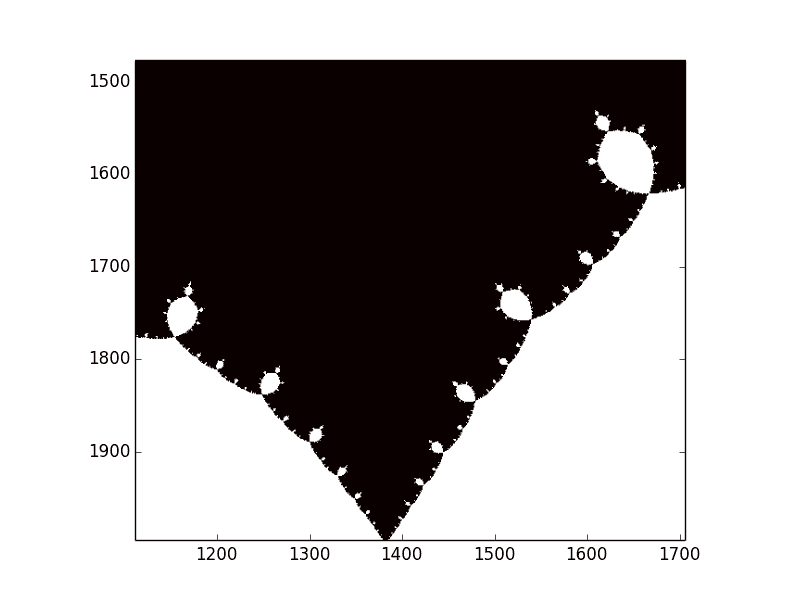
second-attempt-zoomed2
It’s pretty incredible, and a huge question is jumping out at me: what the heck is causing this pattern to occur? What secret does -1 know that +1 doesn’t that makes the resulting pattern so intricate?
But an even bigger question is this. We just discovered that some values of $ c$ make $ z \mapsto z^2 + c$ result in interesting patterns, and some do not! So the question is which ones make interesting patterns? Even if we just, say, fix the starting point to zero: what is the pattern in the complex numbers that would tell me when this transformation makes zero blow up, and when it keeps zero small?
Sounds like a job for another program. This time we’ll use a nice little Python feature called a closure, which we define a function that saves the information that exists when it’s created for later. It will let us write a function that takes in $ c$ and produces a function that transforms according to $ z \mapsto z^2+c$.
def squarePlusC(c):
def f(z):
return z*z + c
return f
And we can use the very same classification/graphing function from before to do this.
def classifySquarePlusC(c):
return isSmallForever(0, squarePlusC(c))
grid = classify(classifySquarePlusC, xRange=(-2, 1), yRange=(-1, 1), step=0.005)
gridToImage(grid)
And the result:
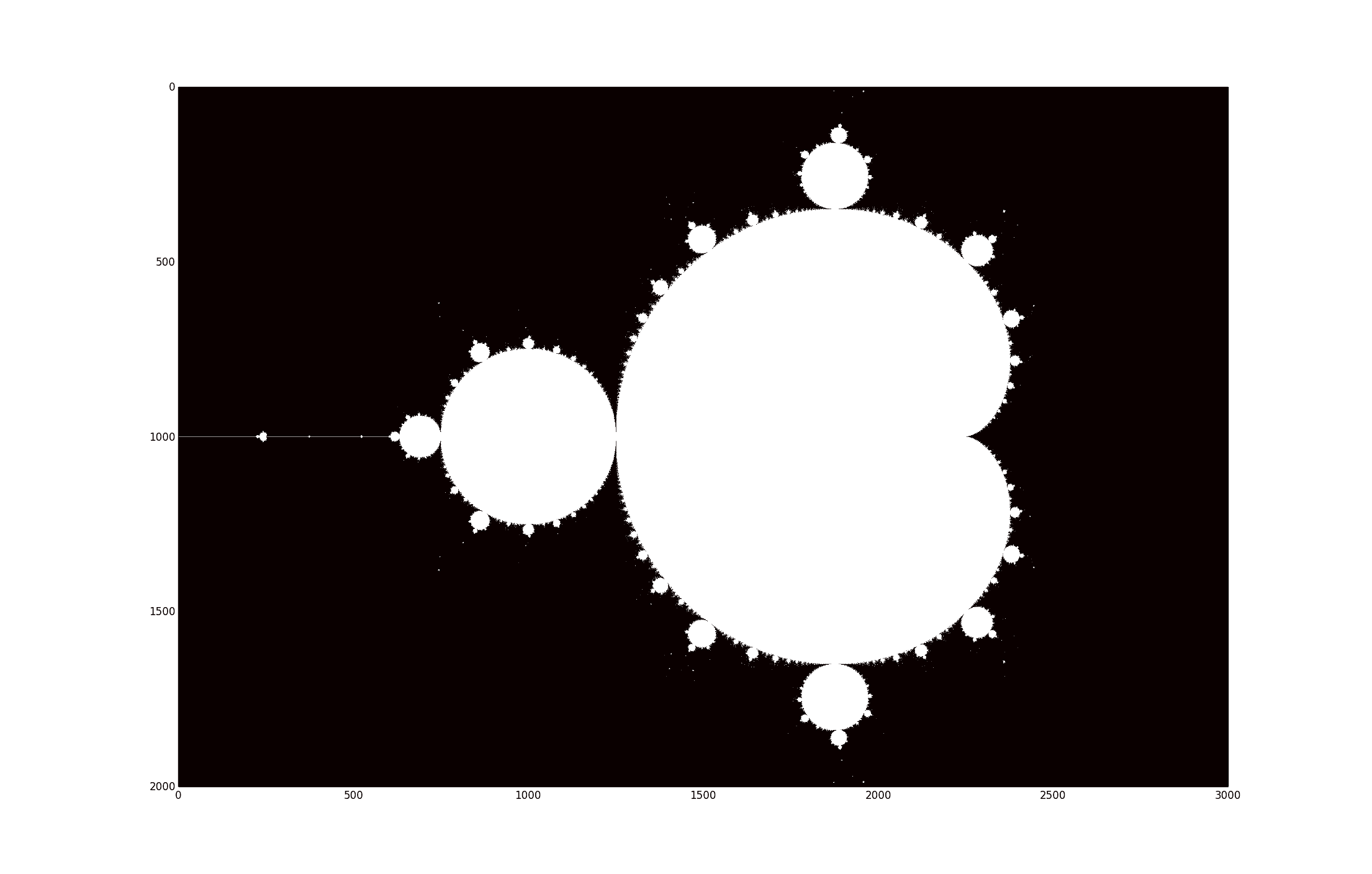
mandelbrot
Stunning. This wonderful pattern, which is still largely not understood today, is known as the Mandelbrot set. That is, the white points are the points in the Mandlebrot set, and the black points are not in it. The detail on the border of this thing is infinitely intricate. For example, we can change the window in our little program to zoom in on a particular region.
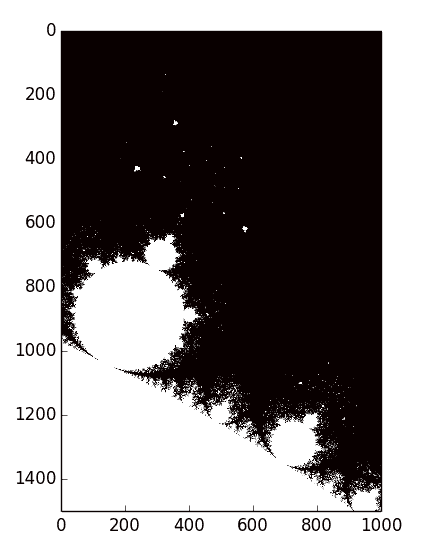
mandelbrot-zoomed
And if you keep zooming in you keep getting more and more detail. This was true of the specific case of $ z^2 – 1$, but somehow the patterns in the Mandelbrot set are much more varied and interesting. And if you keep going down eventually you’ll see patterns that look like the original Mandelbrot set. We can already kind of see that happening above. The name for this idea is a fractal, and the $ z^2 – 1$ image has it too. Fractals are a fascinating and mysterious subject studied in a field called discrete dynamical systems. Many people dedicate their entire lives to studying these things, and it’s for good reason. There’s a lot to learn and even more that’s unknown!
So this is the end of our journey for now. I’ve posted all of the code we used in the making of this post so you can continue to play, but here are some interesting ideas.
- The Mandelbrot set (and most fractals) are usually colored. The way they’re colored is as follows. Rather than just say true or false when zero blows up beyond 2 in length, you return the number of iterations $ k$ that happened. Then you pick a color based on how big $ k$ is. There’s a link below that lets you play with this. In fact, adding colors shows that there is even more intricate detail happening outside the Mandelbrot set that’s too faint to see in our pictures above. Such as this.
- Some very simple questions about fractals are very hard to answer. For example, is the Mandelbrot set connected? That is, is it possible to “walk” from every point in the Mandelbrot set to every other point without leaving the set? Despite the scattering of points in the zoomed in picture above that suggest the answer is no, the answer is actually yes! This is a really difficult thing to prove, however.
- The patterns in many fractals are often used to generate realistic looking landscapes and generate pseudo randomness. So fractals are not just mathematical curiosities.
- You should definitely be experimenting with this stuff! What happens if you change the length threshold from 2 to some bigger number? What about a smaller number? What if you do powers different than $ 2$? There’s so much to explore!
- The big picture thing to take away from this is that it’s not the numbers themselves that are particularly interesting, it’s the transformations of the numbers that generate these patterns! The interesting questions are what kinds of things are the same under these transformations, and what things are different. This is a very general idea in mathematics, and the more math you do the more you’ll find yourself wondering about useful and bizarre transformations.
For the chance to keep playing with the Mandelbrot set, check out this Mandelbrot grapher that works in your browser. It lets you drag rectangles to zoom further in on regions of interest. It’s really fun.
Until next time!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.