Greedy algorithms are by far one of the easiest and most well-understood algorithmic techniques. There is a wealth of variations, but at its core the greedy algorithm optimizes something using the natural rule, “pick what looks best” at any step. So a greedy routing algorithm would say to a routing problem: “You want to visit all these locations with minimum travel time? Let’s start by going to the closest one. And from there to the next closest one. And so on.”
Because greedy algorithms are so simple, researchers have naturally made a big effort to understand their performance. Under what conditions will they actually solve the problem we’re trying to solve, or at least get close? In a previous post we gave some easy-to-state conditions under which greedy gives a good approximation, but the obvious question remains: can we characterize when greedy algorithms give an optimal solution to a problem?
The answer is yes, and the framework that enables us to do this is called a matroid. That is, if we can phrase the problem we’re trying to solve as a matroid, then the greedy algorithm is guaranteed to be optimal. Let’s start with an example when greedy is provably optimal: the minimum spanning tree problem. Throughout the article we’ll assume the reader is familiar with the very basics of linear algebra and graph theory (though we’ll remind ourselves what a minimum spanning tree is shortly). For a refresher, this blog has primers on both subjects. But first, some history.
History
Matroids were first introduced by Hassler Whitney in 1935, and independently discovered a little later by B.L. van der Waerden (a big name in combinatorics). They were both interested in devising a general description of “independence,” the properties of which are strikingly similar when specified in linear algebra and graph theory. Since then the study of matroids has blossomed into a large and beautiful theory, one part of which is the characterization of the greedy algorithm: greedy is optimal on a problem if and only if the problem can be represented as a matroid. Mathematicians have also characterized which matroids can be modeled as spanning trees of graphs (we will see this momentarily). As such, matroids have become a standard topic in the theory and practice of algorithms.
Minimum Spanning Trees
It is often natural in an undirected graph $G = (V,E)$ to find a connected subset of edges that touch every vertex. As an example, if you’re working on a power network you might want to identify a “backbone” of the network so that you can use the backbone to cheaply travel from any node to any other node. Similarly, in a routing network (like the internet) it costs a lot of money to lay down cable, it’s in the interest of the internet service providers to design analogous backbones into their infrastructure.
A minimal subset of edges in a backbone like this is guaranteed to form a tree. This is simply because if you have a cycle in your subgraph then removing any edge on that cycle doesn’t break connectivity or the fact that you can get from any vertex to any other (and trees are the maximal subgraphs without cycles). As such, these “backbones” are called spanning trees. “Span” here means that you can get from any vertex to any other vertex, and it suggests the connection to linear algebra that we’ll describe later, and it’s a simple property of a tree that there is a unique path between any two vertices in the tree.
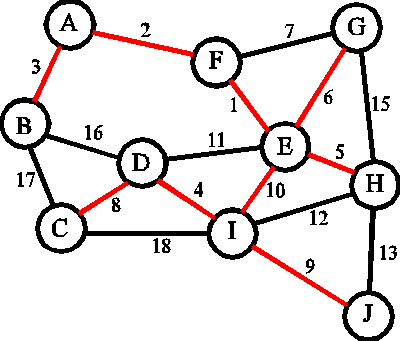
An example of a spanning tree
When your edges $e \in E$ have nonnegative weights $w_e \in \mathbb{R}^{\geq 0}$, we can further ask to find a minimum cost spanning tree. The cost of a spanning tree $T$ is just the sum of its edges, and it’s important enough of a definition to offset.
Definition: A minimum spanning tree $T$ of a weighted graph $G$ (with weights $w_e \geq 0$ for $e \in E$) is a spanning tree which minimizes the quantity
$$w(T) = \sum_{e \in T} w_e$$There are a lot of algorithms to find minimal spanning trees, but one that will lead us to matroids is Kruskal’s algorithm. It’s quite simple. We’ll maintain a forest $F$ in $G$, which is just a subgraph consisting of a bunch of trees that may or may not be connected. At the beginning $F$ is just all the vertices with no edges. And then at each step we add to $F$ the edge $e$ whose weight is smallest and also does not introduce any cycles into $F$. If the input graph $G$ is connected then this will always produce a minimal spanning tree.
Theorem: Kruskal’s algorithm produces a minimal spanning tree of a connected graph.
Proof. Call $F_t$ the forest produced at step $t$ of the algorithm. Then $F_0$ is the set of all vertices of $G$ and $F_{n-1}$ is the final forest output by Kruskal’s (as a quick exercise, prove all spanning trees on $n$ vertices have $n-1$ edges, so we will stop after $n-1$ rounds). It’s clear that $F_{n-1}$ is a tree because the algorithm guarantees no $F_i$ will have a cycle. And any tree with $n-1$ edges is necessarily a spanning tree, because if some vertex were left out then there would be $n-1$ edges on a subgraph of $n-1$ vertices, necessarily causing a cycle somewhere in that subgraph.
Now we’ll prove that $F_{n-1}$ has minimal cost. We’ll prove this in a similar manner to the general proof for matroids. Indeed, say you had a tree $T$ whose cost is strictly less than that of $F_{n-1}$ (we can also suppose that $T$ is minimal, but this is not necessary). Pick the minimal weight edge $e \in T$ that is not in $F_{n-1}$. Adding $e$ to $F_{n-1}$ introduces a unique cycle $C$ in $F_{n-1}$. This cycle has some strange properties. First, $e$ has the highest cost of any edge on $C$. For otherwise, Kruskal’s algorithm would have chosen it before the heavier weight edges. Second, there is another edge in $C$ that’s not in $T$ (because $T$ was a tree it can’t have the entire cycle). Call such an edge $e’$. Now we can remove $e’$ from $F_{n-1}$ and add $e$. This can only increase the total cost of $F_{n-1}$, but this transformation produces a tree with one more edge in common with $T$ than before. This contradicts that $T$ had strictly lower weight than $F_{n-1}$, because repeating the process we described would eventually transform $F_{n-1}$ into $T$ exactly, while only increasing the total cost.
$$\square$$Just to recap, we defined sets of edges to be “good” if they did not contain a cycle, and a spanning tree is a maximal set of edges with this property. In this scenario, the greedy algorithm performed optimally at finding a spanning tree with minimal total cost.
Columns of Matrices
Now let’s consider a different kind of problem. Say I give you a matrix like this one:
$$\displaystyle A = \begin{pmatrix} 2 & 0 & 1 & -1 & 0 \\\ 0 & -4 & 0 & 1 & 0 \\\ 0 & 0 & 1 & 0 & 7 \end{pmatrix}$$In the standard interpretation of linear algebra, this matrix represents a linear function $f$ from one vector space $V$ to another $W$, with the basis $(v_1, \dots, v_5)$ of $V$ being represented by columns and the basis $(w_1, w_2, w_3)$ of $W$ being represented by the rows. Column $j$ tells you how to write $f(v_j)$ as a linear combination of the $w_i$, and in so doing uniquely defines $f$.
Now one thing we want to calculate is the rank of this matrix. That is, what is the dimension of the image of $V$ under $f$? By linear algebraic arguments we know that this is equivalent to asking “how many linearly independent columns of $A$ can we find”? An interesting consequence is that if you have two sets of columns that are both linearly independent and maximally so (adding any other column to either set would necessarily introduce a dependence in that set), then these two sets have the same size. This is part of why the rank of a matrix is well-defined.
If we were to give the columns of $A$ costs, then we could ask about finding the minimal-cost maximally-independent column set. It sounds like a mouthful, but it’s exactly the same idea as with spanning trees: we want a set of vectors that spans the whole column space of $A$, but contains no “cycles” (linearly dependent combinations), and we want the cheapest such set.
So we have two kinds of “independence systems” that seem to be related. One interesting question we can ask is whether these kinds of independence systems are “the same” in a reasonable way. Hardcore readers of this blog may see the connection quite quickly. For any graph $G = (V,E)$, there is a natural linear map from $E$ to $V$, so that a linear dependence among the columns (edges) corresponds to a cycle in $G$. This map is called the incidence matrix by combinatorialists and the first boundary map by topologists.
The map is easy to construct: for each edge $e = (v_i,v_j)$ you add a column with a 1 in the $j$-th row and a $-1$ in the $i$-th row. Then taking a sum of edges gives you zero if and only if the edges form a cycle. So we can think of a set of edges as “independent” if they don’t contain a cycle. It’s a little bit less general than independence over $\mathbb{R}$, but you can make it exactly the same kind of independence if you change your field from real numbers to $\mathbb{Z}/2\mathbb{Z}$. We won’t do this because it will detract from our end goal (to analyze greedy algorithms in realistic settings), but for further reading this survey of Oxley assumes that perspective.
So with the recognition of how similar these notions of independence are, we are ready to define matroids.
The Matroid
So far we’ve seen two kinds of independence: “sets of edges with no cycles” (also called forests) and “sets of linearly independent vectors.” Both of these share two trivial properties: there are always nonempty independent sets, and every subset of an independent set is independent. We will call any family of subsets with this property an independence system.
Definition: Let $X$ be a finite set. An independence system over $X$ is a family $\mathscr{I}$ of subsets of $X$ with the following two properties.
- $\mathscr{I}$ is nonempty.
- If $I \in \mathscr{I}$, then so is every subset of $I$.
This is too general to characterize greedy algorithms, so we need one more property shared by our examples. There are a few things we do, but here’s one nice property that turns out to be enough.
Definition: A matroid $M = (X, \mathscr{I})$ is a set $X$ and an independence system $\mathscr{I}$ over $X$ with the following property:
If $A, B$ are in $\mathscr{I}$ with $|A| = |B| + 1$, then there is an element $x \in A \setminus B$ such that $B \cup \{ a \} \in \mathscr{I}$.
In other words, this property says if I have an independent set that is not maximally independent, I can grow the set by adding some suitably-chosen element from a larger independent set. We’ll call this the extension property. For a warmup exercise, let’s prove that the extension property is equivalent to the following (assuming the other properties of a matroid):
For every subset $Y \subset X$, all maximal independent sets contained in $Y$ have equal size.
Proof. For one direction, if you have two maximal sets $A, B \subset Y \subset X$ that are not the same size (say $A$ is bigger), then you can take any subset of $A$ whose size is exactly $|B| + 1$, and use the extension property to make $B$ larger, a contradiction. For the other direction, say that I know all maximal independent sets of any $Y \subset X$ have the same size, and you give me $A, B \subset X$. I need to find an $a \in A \setminus B$ that I can add to $B$ and keep it independent. What I do is take the subset $Y = A \cup B$. Now the sizes of $A, B$ don’t change, but $B$ can’t be maximal inside $Y$ because it’s smaller than $A$ ($ A$ might not be maximal either, but it’s still independent). And the only way to extend $B$ is by adding something from $A$, as desired.
$$\square$$So we can use the extension property and the cardinality property interchangeably when talking about matroids. Continuing to connect matroid language to linear algebra and graph theory, the maximal independent sets of a matroid are called bases, the size of any basis is the rank of the matroid, and the minimal dependent sets are called circuits. In fact, you can characterize matroids in terms of the properties of their circuits, which are dual to the properties of bases (and hence all independent sets) in a very concrete sense.
But while you could spend all day characterizing the many kinds of matroids and comatroids out there, we are still faced with the task of seeing how the greedy algorithm performs on a matroid. That is, suppose that your matroid $M = (X, \mathscr{I})$ has a nonnegative real number $w(x)$ associated with each $x \in X$. And suppose we had a black-box function to determine if a given set $S \subset X$ is independent. Then the greedy algorithm maintains a set $B$, and at every step adds a minimum weight element that maintains the independence of $B$. If we measure the cost of a subset by the sum of the weights of its elements, then the question is whether the greedy algorithm finds a minimum weight basis of the matroid.
The answer is even better than yes. In fact, the answer is that the greedy algorithm performs perfectly if and only if the problem is a matroid! More rigorously,
Theorem: Suppose that $M = (X, \mathscr{I})$ is an independence system, and that we have a black-box algorithm to determine whether a given set is independent. Define the greedy algorithm to iteratively adds the cheapest element of $X$ that maintains independence. Then the greedy algorithm produces a maximally independent set $S$ of minimal cost for every nonnegative cost function on $X$, if and only if $M$ is a matroid.
It’s clear that the algorithm will produce a set that is maximally independent. The only question is whether what it produces has minimum weight among all maximally independent sets. We’ll break the theorem into the two directions of the “if and only if”:
Part 1: If $M$ is a matroid, then greedy works perfectly no matter the cost function. Part 2: If greedy works perfectly for every cost function, then $M$ is a matroid.
Proof of Part 1.
Call the cost function $w : X \to \mathbb{R}^{\geq 0}$, and suppose that the greedy algorithm picks elements $B = \{ x_1, x_2, \dots, x_r \}$ (in that order). It’s easy to see that $w(x_1) \leq w(x_2) \leq \dots \leq w(x_r)$. Now if you give me any list of $r$ independent elements $y_1, y_2, \dots, y_r \in X$ that has $w(y_1) \leq \dots \leq w(y_r)$, I claim that $w(x_i) \leq w(y_i)$ for all $i$. This proves what we want, because if there were a basis of size $r$ with smaller weight, sorting its elements by weight would give a list contradicting this claim.
To prove the claim, suppose to the contrary that it were false, and for some $k$ we have $w(x_k) > w(y_k)$. Moreover, pick the smallest $k$ for which this is true. Note $k > 1$, and so we can look at the special sets $S = \{ x_1, \dots, x_{k-1} \}$ and $T = \{ y_1, \dots, y_k \}$. Now $|T| = |S|+1$, so by the matroid property there is some $j$ between $1$ and $r$ so that $S \cup \{ y_j \}$ is an independent set (and $y_j$ is not in $S$). But then $w(y_j) \leq w(y_k) < w(x_k)$, and so the greedy algorithm would have picked $y_j$ before it picks $x_k$ (and the strict inequality means they’re different elements). This contradicts how the greedy algorithm runs, and hence proves the claim.
Proof of Part 2.
We’ll prove this contrapositively as follows. Suppose we have our independence system and it doesn’t satisfy the last matroid condition. Then we’ll construct a special weight function that causes the greedy algorithm to fail. So let $A,B$ be independent sets with $|A| = |B| + 1$, but for every $a \in A \setminus B$ adding $a$ to $B$ never gives you an independent set.
Now what we’ll do is define our weight function so that the greedy algorithm picks the elements we want in the order we want (roughly). In particular, we’ll assign all elements of $A \cap B$ a tiny weight we’ll call $w_1$. For elements of $B – A$ we’ll use $w_2$, and for $A – B$ we’ll use $w_3$, with $w_4$ for everything else. In a more compact notation:
\[ w(x) = \begin{cases} w_1 & \textup{if } x \in A \cap B \\ w_2 & \textup{if } x \in B - A \\ w_3 & \textup{if } x \in A - B \\ w_4 & \textup{otherwise} \end{cases} \]We need two things for this weight function to screw up the greedy algorithm. The first is that $w_1 < w_2 < w_3 < w_4$, so that greedy picks the elements in the order we want. Note that this means it’ll first pick all of $A \cap B$, and then all of $B – A$, and by assumption it won’t be able to pick anything from $A – B$, but since $B$ is assumed to be non-maximal, we have to pick at least one element from $X – (A \cup B)$ and pay $w_4$ for it.
So the second thing we want is that the cost of doing greedy is worse than picking any maximally independent set that contains $A$ (and we know that there has to be some maximal independent set containing $A$). In other words, if we call $m$ the size of a maximally independent set, we want
$$\displaystyle |A \cap B| w_1 + |B-A|w_2 + (m – |B|)w_4 > |A \cap B|w_1 + |A-B|w_3 + (m-|A|)w_4$$This can be rearranged (using the fact that $|A| = |B|+1$) to
$$\displaystyle w_4 > |A-B|w_3 – |B-A|w_2$$The point here is that the greedy picks too many elements of weight $w_4$, since if we were to start by taking all of $A$ (instead of all of $B$), then we could get by with one fewer. That might not be optimal, but it’s better than greedy and that’s enough for the proof.
So we just need to make $w_4$ large enough to make this inequality hold, while still maintaining $w_2 < w_3$. There are probably many ways to do this, and here’s one. Pick some $0 < \varepsilon < 1$, and set
\[ \begin{aligned} w_1 &= \varepsilon / |X| \\ w_2 &= \varepsilon / |B-A| \\ w_3 &= (1 + \varepsilon) / |A-B| \\ w_4 &= 2 \end{aligned} \]It’s trivial that $w_1 < w_2$ and $w_3 < w_4$. For the rest we need some observations. First, the fact that $|A-B| = |B-A| + 1$ implies that $w_2 < w_3$. Second, both $|A-B|$ and $|B-A|$ are nonempty, since otherwise the second property of independence systems would contradict our assumption that augmenting $B$ with elements of $A$ breaks independence. Using this, we can divide by these quantities to get
$$\displaystyle w_4 = 2 > 1 = \frac{|A-B|(1 + \varepsilon)}{|A-B|} – \frac{|B-A|\varepsilon}{|B-A|}$$This proves the claim and finishes the proof.
$$\square$$As a side note, we proved everything here with respect to minimizing the sum of the weights, but one can prove an identical theorem for maximization. The only part that’s really different is picking the clever weight function in part 2. In fact, you can convert between the two by defining a new weight function that subtracts the old weights from some fixed number $N$ that is larger than any of the original weights. So these two problems really are the same thing.
This is pretty amazing! So if you can prove your problem is a matroid then you have an awesome algorithm automatically. And if you run the greedy algorithm for fun and it seems like it works all the time, then that may be hinting that your problem is a matroid. This is one of the best situations one could possibly hope for.
But as usual, there are a few caveats to consider. They are both related to efficiency. The first is the black box algorithm for determining if a set is independent. In a problem like minimum spanning tree or finding independent columns of a matrix, there are polynomial time algorithms for determining independence. These two can both be done, for example, with Gaussian elimination. But there’s nothing to stop our favorite matroid from requiring an exponential amount of time to check if a set is independent. This makes greedy all but useless, since we need to check for independence many times in every round.
Another, perhaps subtler, issue is that the size of the ground set $X$ might be exponentially larger than the rank of the matroid. In other words, at every step our greedy algorithm needs to find a new element to add to the set it’s building up. But there could be such a huge ocean of candidates, all but a few of which break independence. In practice an algorithm might be working with $X$ implicitly, so we could still hope to solve the problem if we had enough knowledge to speed up the search for a new element.
There are still other concerns. For example, a naive approach to implementing greedy takes quadratic time, since you may have to look through every element of $X$ to find the minimum-cost guy to add. What if you just have to have faster runtime than $O(n^2)$? You can still be interested in finding more efficient algorithms that still perform perfectly, and to the best of my knowledge there’s nothing that says that greedy is the only exact algorithm for your favorite matroid. And then there are models where you don’t have direct/random access to the input, and lots of other ways that you can improve on greedy. But those stories are for another time.
Until then!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.