Tai-Danae Bradley is one of the hosts of PBS Infinite Series, a delightful series of vignettes into fun parts of math. The video below is about the same of SET, a favorite among mathematicians. Specifically, Tai-Danae explains how SET cards lie in (using more technical jargon) a vector space over a finite field, and that valid sets correspond to lines. If you don’t immediately know how this would work, watch the video.
In this post I want to share a parlor trick for SET that I originally heard from Charlotte Chan. It uses the same ideas from the video above, which I’ll only review briefly.
In the game of SET you see a board of cards like the following, and players look for sets.

Image source: theboardgamefamily.com
A valid set is a triple of cards where, feature by feature, the characteristics on the cards are either all the same or all different. A valid set above is {one empty blue oval, two solid blue ovals, three shaded blue ovals}. The feature of “fill” is different on all the cards, but the feature of “color” is the same, etc.
In a game of SET, the cards are dealt in order from a shuffled deck, players race to claim sets, removing the set if it’s valid, and three cards are dealt to replace the removed set. Eventually the deck is exhausted and the game is over, and the winner is the player who collected the most sets.
There are a handful of mathematical tricks you can use to help you search for sets faster, but the parlor trick in this post adds a fun variant to the end of the game.
Play the game of SET normally, but when you get down to the last card in the deck, don’t reveal it. Keep searching for sets until everyone agrees no visible sets are left. Then you start the variant: the first player to guess the last un-dealt card in the deck gets a bonus set.
The math comes in when you discover that you don’t need to guess, or remember anything about the game that was just played! A clever stranger could walk into the room at the end of the game and win the bonus point.
Theorem: As long as every player claimed a valid set throughout the game, the information on the remaining board uniquely determines the last (un-dealt) card.
Before we get to the proof, some reminders. Recall that there are four features on a SET card, each of which has three options. Enumerate the options for each feature (e.g., {Squiggle, Oval, Diamond} = {0, 1, 2}).
While we will not need the geometry induced by this, this implies each card is a vector in the vector space $ \mathbb{F}_3^4$, where $ \mathbb{F}_3 = \mathbb{Z}/3\mathbb{Z}$ is the finite field of three elements, and the exponent means “dimension 4.” As Tai-Danae points out in the video, each SET is an affine line in this vector space. For example, if this is the enumeration:
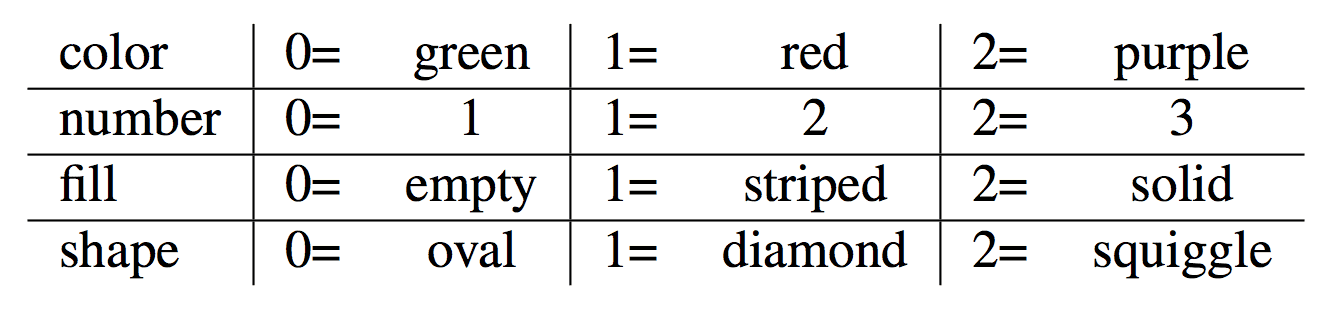
Source: “[The Joy of Set](https://www.setgame.com/sites/default/files/teacherscorner/THE%20JOY%20OF%20SET.pdf)“
Then using the enumeration, a set might be given by
$$\displaystyle \{ (1, 1, 1, 1), (1, 2, 0, 1), (1, 0, 2, 1) \}$$The crucial feature for us is that the vector-sum (using the modular field arithmetic on each entry) of the cards in a valid set is the zero vector $ (0, 0, 0, 0)$. This is because $ 1+1+1 = 0, 2+2+2 = 0,$ and $ 1+2+3=0$ are all true mod 3.
Proof of Theorem. Consider the vector-valued invariant $ S_t$ equal to the sum of the remaining cards after $ t$ sets have been taken. At the beginning of the game the deck has 81 cards that can be partitioned into valid sets. Because each valid set sums to the zero vector, $ S_0 = (0, 0, 0, 0)$. Removing a valid set via normal play does not affect the invariant, because you’re subtracting a set of vectors whose sum is zero. So $ S_t = 0$ for all $ t$.
At the end of the game, the invariant still holds even if there are no valid sets left to claim. Let $ x$ be the vector corresponding to the last un-dealt card, and $ c_1, \dots, c_n$ be the remaining visible cards. Then $ x + \sum_{i=1}^n c_i = (0,0,0,0)$, meaning $ x = -\sum_{i=1}^n c_i$.
$$\square$$I would provide an example, but I want to encourage everyone to play a game of SET and try it out live!
Charlotte, who originally showed me this trick, was quick enough to compute this sum in her head. So were the other math students we played SET with. It’s a bit easier than it seems since you can do the sum feature by feature. Even though I’ve known about this trick for years, I still require a piece of paper and a few minutes.
Because this is Math Intersect Programming, the reader is encouraged to implement this scheme as an exercise, and simulate a game of SET by removing randomly chosen valid sets to verify experimentally that this scheme works.
Until next time!
Want to respond? Send me an email, post a webmention, or find me elsewhere on the internet.